Zero/one-inflated Beta regression

Key points
  • The Beta distribution represents a proportion between 0 and 1, but does not include 0 or 1. Zero/one-inflated Beta regression models separate processes for the 0s and 1s
library(tidyverse)
library(marginaleffects)
library(brms)
library(tidybayes)
library(parameters)
library(tinytable)
library(patchwork)
library(extraDistr)
library(ggridges)
library(scales)
library(betareg)

# Data via the WHO via Kaggle
# https://www.kaggle.com/datasets/lsind18/who-immunization-coverage
tetanus <- readRDS("data/data-processed/tetanus_pab.rds")
tetanus_2020 <- tetanus |> 
  filter(year == 2020) |> 
  # Cheat a little
  mutate(prop_pab = ifelse(prop_pab >= 0.97, 1, prop_pab)) |> 
  # Reverse this
  mutate(prop_unvacc = 1 - prop_pab)

theme_set(theme_minimal())

options(mc.cores = 4)  # Use 4 cores for {brms}

Distribution intuition

The Beta distribution is great for proportions, but it doesn’t work with values that are exactly 0 or 1.

To get around this, we can use a special zero-inflated Beta regression. We’ll still model the \(\mu\) (mu) and \(\phi\) (phi) (or mean and precision) of the beta distribution, but we’ll also model one new special parameter \(\pi\) (pi; not 3.14, though). With zero-inflated regression, we’re actually modelling a mixture of data-generating processes:

  1. A logistic regression model that predicts if an outcome is 0 or not, defined by \(\pi\)
  2. A Beta regression model that predicts if an outcome is between 0 and 1 if it’s not zero, defined by \(\mu\) and \(\phi\)

In general, the model looks like this:

\[ \begin{aligned} Y_i &\sim \operatorname{Zero-inflated\ Beta}(\pi_i, \mu_i, \phi_i) \\ \operatorname{logit}(\pi_i) &= \gamma_0 + \gamma \mathbf{X}_i & \text{on/off process} \\ \operatorname{logit}(\mu_i) &= \beta_0 + \beta \mathbf{X}_i & \gt 0 \text{ process} \\ \log(\phi_i) &= \eta_0 + \eta \mathbf{X}_i & \text{dispersion} \end{aligned} \]

Example: Modeling the proprotion of tetanus non-vaccinations

To illustrate this, we’ll look at 2020 PAB tetanus vaccination rates, since far more countries have reached or are approaching universal coverage. We’ll also cheat a little, since only 3 countries are actually at 100%—for the sake of this example, if a country is at 97% or more, we’ll consider that 100%.

Also, we’ll look at the reverse of the proportion, or the proportion of unvaccinated, since there is no one-inflated regression built into {brms}. Their suggestion is to either flip the value (like we’re doing here) or use zero-one-inflated regression and tell the zero-focused process there to be constant. Flipping the value is easier, so we’ll do that.

Let’s first see how many 0s we’re working with:

tetanus_2020 |> 
  count(prop_unvacc == 0) |> 
  mutate(prop = n / sum(n))
## # A tibble: 2 × 3
##   `prop_unvacc == 0`     n  prop
##   <lgl>              <int> <dbl>
## 1 FALSE                 84 0.792
## 2 TRUE                  22 0.208

20% of the countries are fully vaccinated here (or have 0% unvaccinated kids). The 80% of countries with some unvaccinated children still follows a Beta distribution:

tetanus_2020 |> 
  mutate(is_zero = prop_unvacc == 0) |> 
  mutate(prop_unvacc = ifelse(is_zero, -0.01, prop_unvacc)) |> 
  ggplot(aes(x = prop_unvacc, fill = is_zero)) +
  geom_histogram(binwidth = 0.04, boundary = 0, color = "white") +
  geom_vline(xintercept = 0) +
  scale_x_continuous(labels = label_percent()) +
  scale_fill_viridis_d(
    option = "plasma", end = 0.9,
    guide = guide_legend(reverse = TRUE)
  ) +
  labs(
    x = "Proportion of unvaccinated children", 
    y = "Count", fill = "Is zero?"
  ) +
  theme(legend.position = "bottom")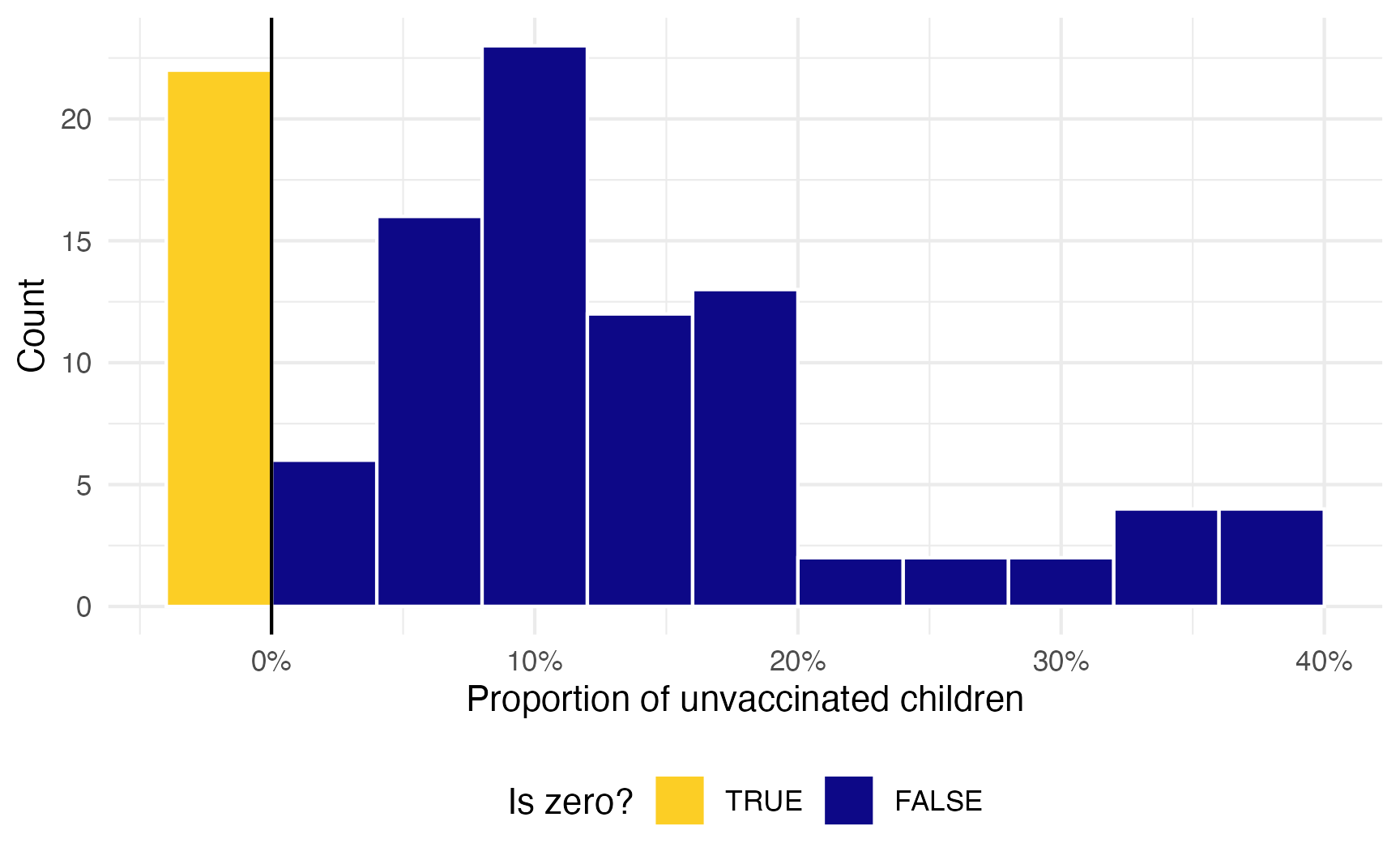

The only difference between regular Beta regression and zero-inflated Beta regression is that we have to specify one more parameter: zi. This corresponds to the \(\pi\) parameter and determines the zero/not-zero process.

To help with the intuition, we’ll first run a model where we don’t actually define a model for zi—it’ll just return the intercept for the \(\pi\) parameter.

priors <- c(
  set_prior("student_t(3, 0, 2.5)", class = "Intercept"),
  set_prior("normal(0, 1)", class = "b"),
  set_prior("logistic(0, 1", class = "Intercept", dpar = "zi")
)
Code 
# Here we log gdp_per_cap because Stan really doesn't like big numbers
model_beta_zi_int_only <- brm(
  bf(
    prop_unvacc ~ log(gdp_per_cap) + region,
    phi ~ 1,
    zi ~ 1
  ),
  data = tetanus_2020,
  family = zero_inflated_beta(),
  prior = priors,
  chains = 4, iter = 2000, seed = 1234,
  file = "models/model_beta_zi_int_only"
)
Code 
model_parameters(model_beta_zi_int_only, verbose = FALSE) |> tt()
Parameter Component Median CI CI_low CI_high pd Rhat ESS
b_Intercept conditional -0.927 0.95 -2.47 0.704 0.87 1 3263
b_phi_Intercept conditional 3.019 0.95 2.68 3.32 1 1 4726
b_loggdp_per_cap conditional -0.144 0.95 -0.35 0.047 0.93 1 3430
b_regionEurope&CentralAsia conditional -0.445 0.95 -1.59 0.428 0.84 1 4109
b_regionLatinAmerica&Caribbean conditional -0.145 0.95 -0.64 0.336 0.72 1 3283
b_regionMiddleEast&NorthAfrica conditional 0.075 0.95 -0.52 0.633 0.6 1 3536
b_regionSouthAsia conditional 0.297 0.95 -0.3 0.893 0.84 1 3213
b_regionSubMSaharanAfrica conditional 0.259 0.95 -0.14 0.68 0.89 1 2602
b_zi_Intercept zero_inflated -1.378 0.95 -1.9 -0.911 1 1 5516

We now have a new parameter here, b_zi_Intercept, or the \(\pi\) in the model. It’s on the logit scale, so we can back-transform it with plogis():

Code 
plogis(-1.39)
## [1] 0.199

That 20%ish represents the number of rows in the dataset with 0 unvaccinated children, which is what we found earlier!

For now, we’ve only done an intercept-only model, but we can model the exact 0/not-0 process. There are probably regional differences (and probably lots of other things) in whether a country is fully vaccinated, so we can include that in the model:

Code 
model_beta_zi <- brm(
  bf(
    prop_unvacc ~ log(gdp_per_cap) + region,
    phi ~ 1,
    zi ~ region
  ),
  data = tetanus_2020,
  family = zero_inflated_beta(),
  prior = priors,
  chains = 4, iter = 2000, seed = 1234,
  file = "models/model_beta_zi"
)

We can look at the individual parts of this model. Here are the posterior predictions of 0s across each region:

# With {marginaleffects}
model_beta_zi |> 
  plot_predictions(condition = c("region", "region"), dpar = "zi") +
  scale_y_continuous(labels = label_percent()) +
  labs(x = NULL, y = "Proportion unvaccinated") +
  scale_color_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  coord_flip()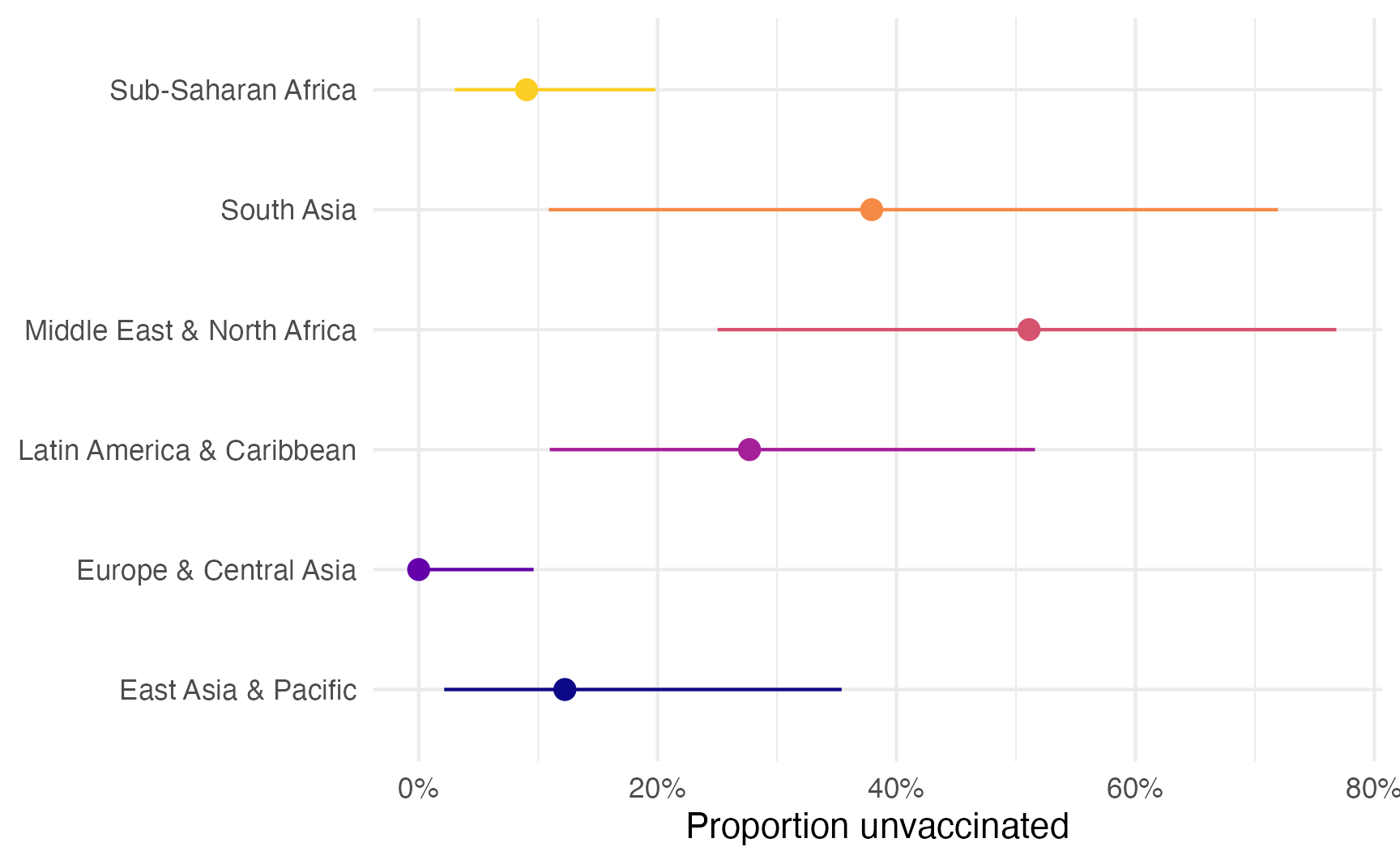 


# With {tidybayes}
model_beta_zi |> 
  linpred_draws(
    newdata = data.frame(gdp_per_cap = 10000, region = unique(tetanus_2020$region)),
    dpar = "zi", transform = TRUE
  ) |> 
  ggplot(aes(y = region, x = zi)) +
  stat_halfeye(aes(fill = region), normalize = "xy") +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  scale_x_continuous(labels = label_percent()) +
  labs(y = NULL, x = "Proportion unvaccinated")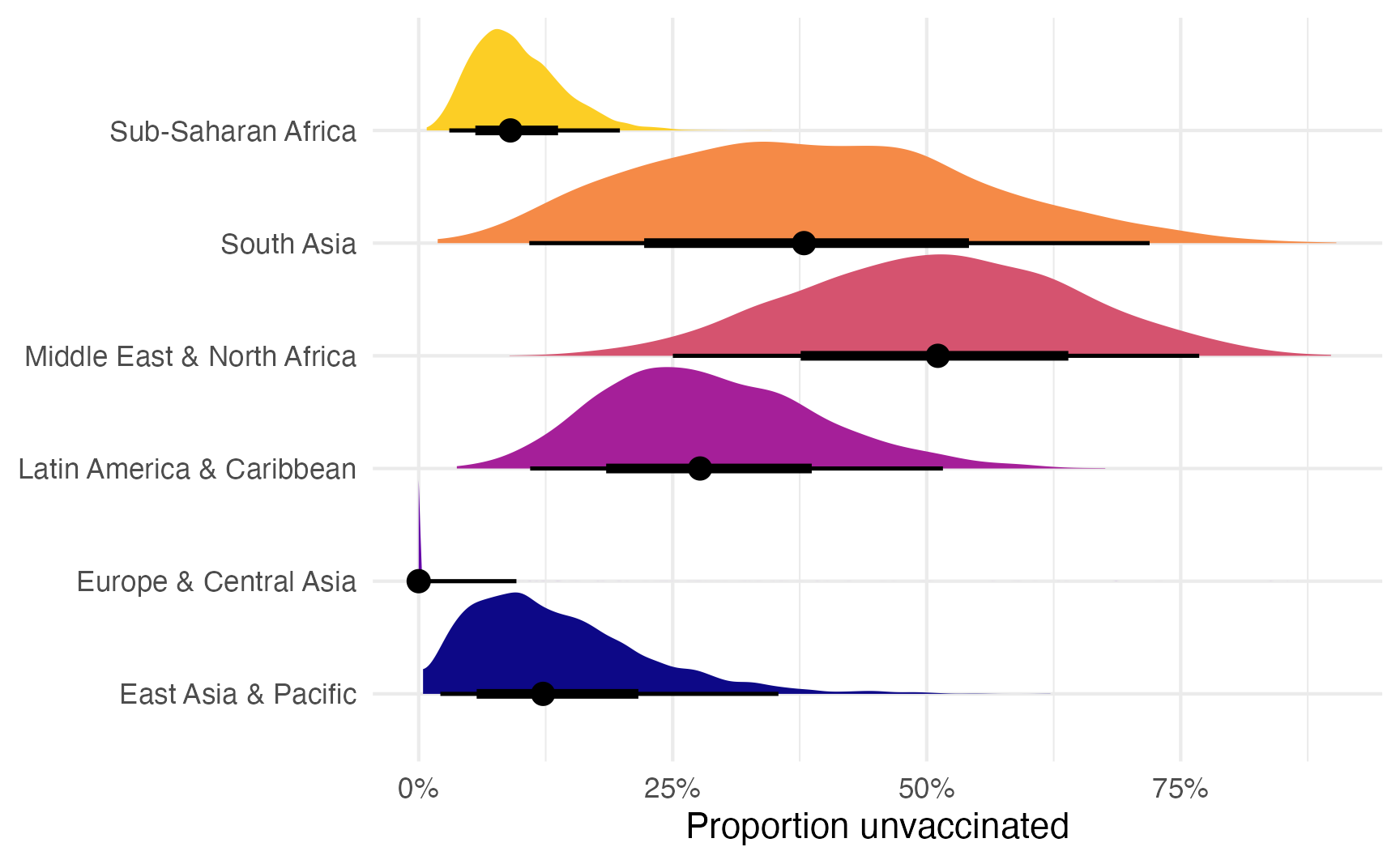

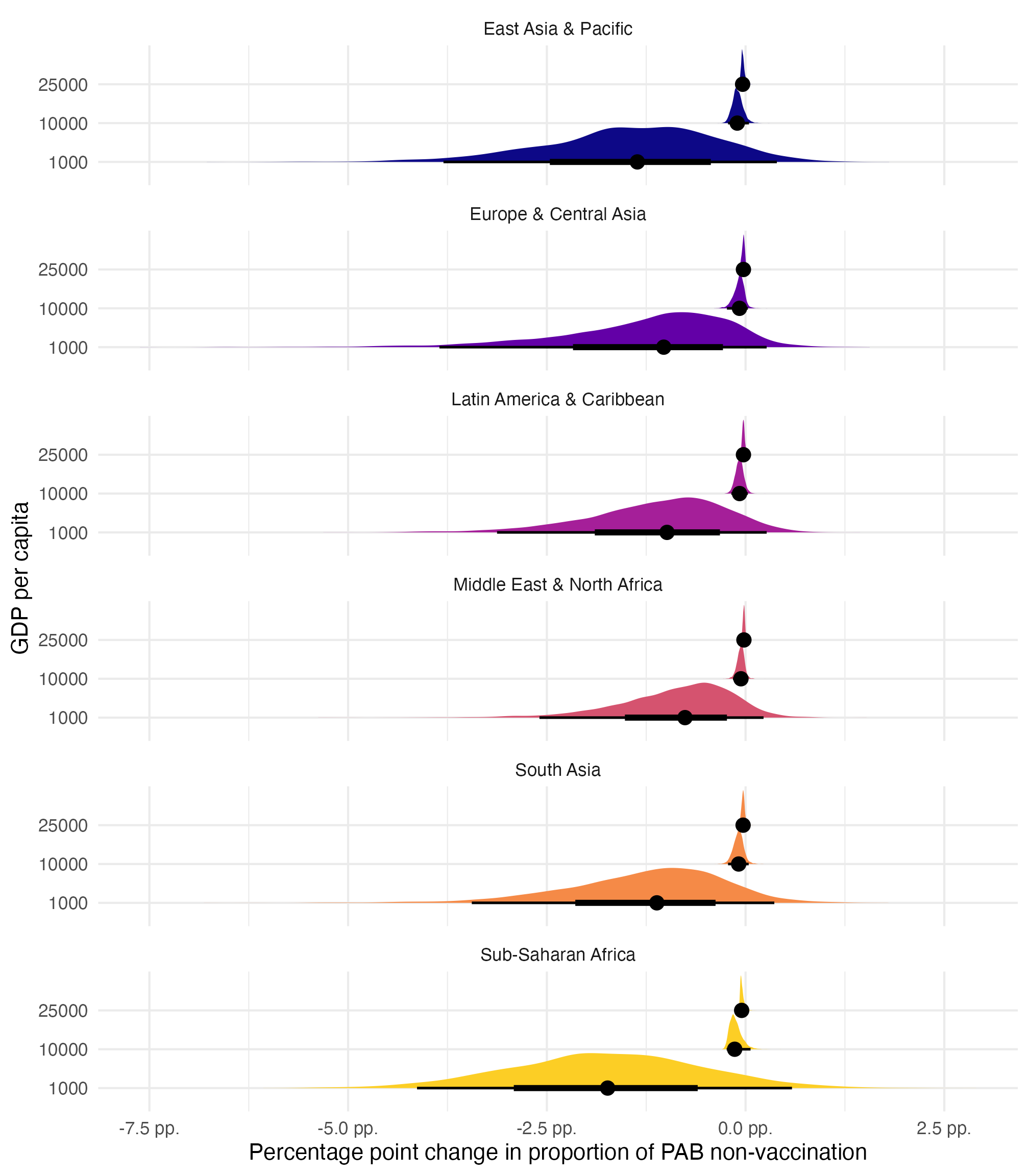
All the regular {marginaleffects} and {tidybayes} functions work too, either on individual parts of the model (with the dpar argument), or on both combined (without any extra arguments). Like this—we can visualize the posterior distributions of the specific marginal effects while also incorporating the 0 process!:

model_beta_zi |> 
  slopes(
    newdata = datagrid(gdp_per_cap = c(1000, 10000, 25000), region = unique),
    variables = "gdp_per_cap"
  ) |> 
  posterior_draws() |> 
  mutate(draw = draw * 1000) |> 
  ggplot(aes(x = draw, y = factor(gdp_per_cap), fill = region)) +
  stat_halfeye(normalize = "xy") +
  scale_x_continuous(labels = label_number(scale = 100, suffix = " pp.")) +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  facet_wrap(vars(region), ncol = 1) +
  labs(
    x = "Percentage point change in proportion of PAB non-vaccination", 
    y = "GDP per capita"
  )

That’s complex and hard! Is there an easier way?

Yeah, kind of! There’s a newer family of model called “ordered beta regression” that automatically deals with the 0 process, 1 process, and in-between process with just one formula instead of specifying separate moving parts for each. Even cooler, it works with any continuous variable with upper and lower bounds, not just things that fit between 0–1 or 0–100.

Citation

Kubinec, Robert. 2022. “Ordered Beta Regression: A Parsimonious, Well-Fitting Model for Continuous Data with Lower and Upper Bounds.” Political Analysis 31, no. 4 (2023): 519–36. https://doi.org/10.1017/pan.2022.20.

See an example of ordered beta regression in action here or here or see the official tutorial here.