library(tidyverse)
library(marginaleffects)
library(brms)
library(tidybayes)
library(parameters)
library(tinytable)
equality <- readRDS("data/data-processed/equality.rds")
clr_dem <- "#1696d2"
clr_gop <- "#db2b27"
clr_ind <- "#fdbf11"
theme_set(theme_minimal())Poisson regression
Modeling \(\lambda\)
We can use regression to model the \(\lambda\) of a Poisson-distributed outcome. In Poisson models, the \(\lambda\) rate must be positive. But if you model \(\lambda\) with a regression model like
\[ \lambda_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots, \]
the predicted values for \(\lambda\) could be negative. So instead we can force \(\lambda\) to be positive by using a log link function, or
\[ \log(\lambda_i) = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots \]
In general, the model looks like this:
\[ \begin{aligned} Y_i &\sim \operatorname{Poisson}(\lambda_i) \\ \log(\lambda_i) &= \beta_0 + \beta \mathbf{X}_i \end{aligned} \]
Example: Modeling the count of LGBTQ+ anti-discrimination laws
We want to model the number of LGBTQ+ anti-discrimination laws in states based on how urban a state is and its historical partisan voting patterns. Here’s the general relationship. A regular straight OLS line doesn’t fit the data well, but because the outcome is a count, and because the general relationship is curvy, Poisson regression will work.
ggplot(equality, aes(x = percent_urban, y = laws)) +
geom_point(aes(fill = historical), pch = 21, size = 4, color = "white") +
geom_smooth(
aes(color = "Poisson regression"), se = FALSE, method = "glm",
method.args = list(family = "poisson")
) +
geom_smooth(aes(color = "OLS regression"), se = FALSE, method = "lm") +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind)) +
scale_color_manual(values = c("#3D9970", "#FF851B")) +
labs(
x = "Percent urban",
y = "Count of laws",
color = NULL,
fill = "Party"
) +
theme(legend.position = "bottom")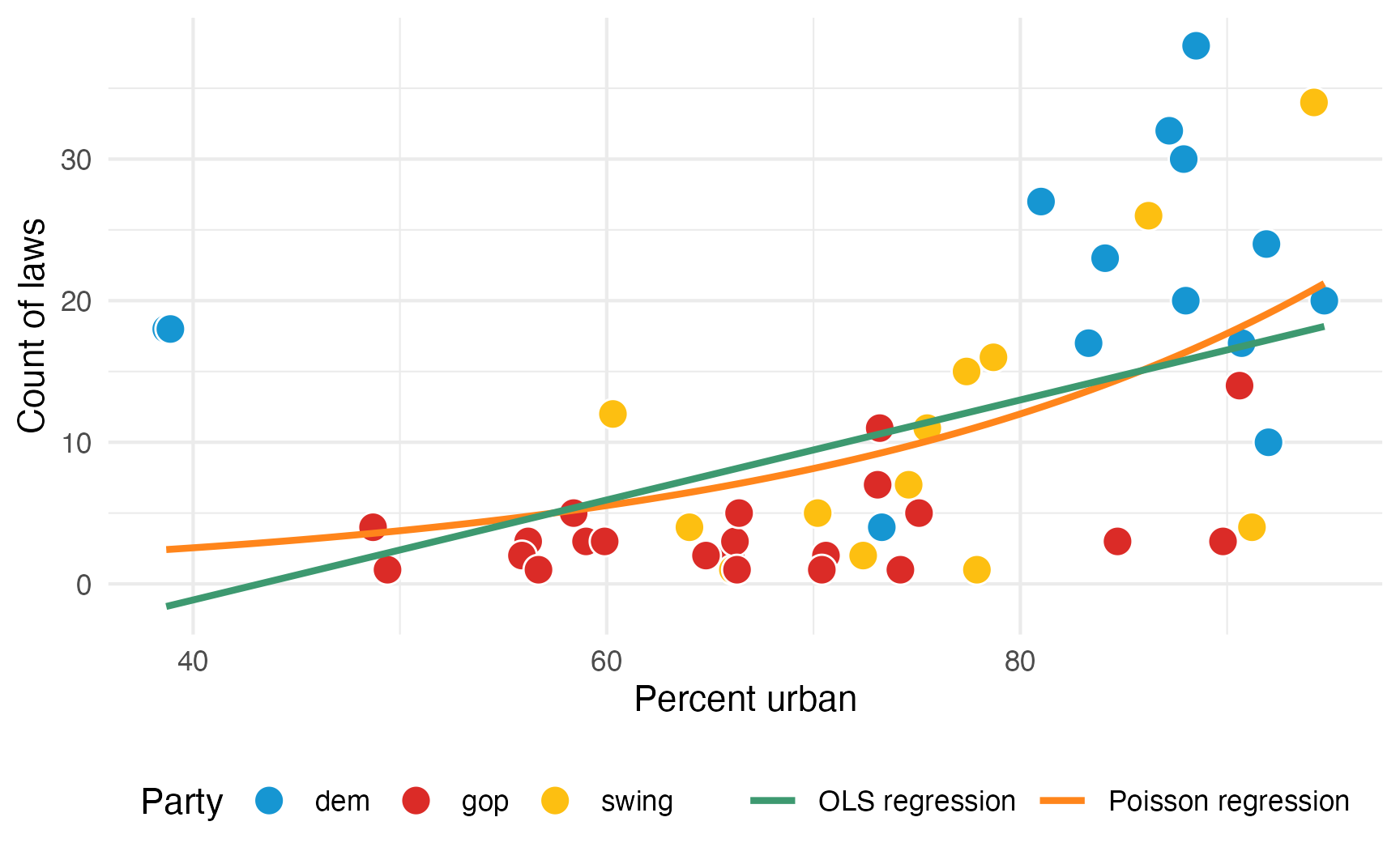
If we model this with regular OLS, we’ll get predictions of negative laws:
model_ols <- lm(laws ~ percent_urban + historical, data = equality)
plot_predictions(model_ols, condition = c("percent_urban", "historical")) +
geom_hline(yintercept = 0) +
geom_point(
data = equality,
aes(x = percent_urban, y = laws, color = historical),
size = 0.75
) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind)) +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind), guide = "none") +
labs(
x = "Percent urban",
y = "Predicted count of laws",
color = "Party"
) +
theme(legend.position = "bottom")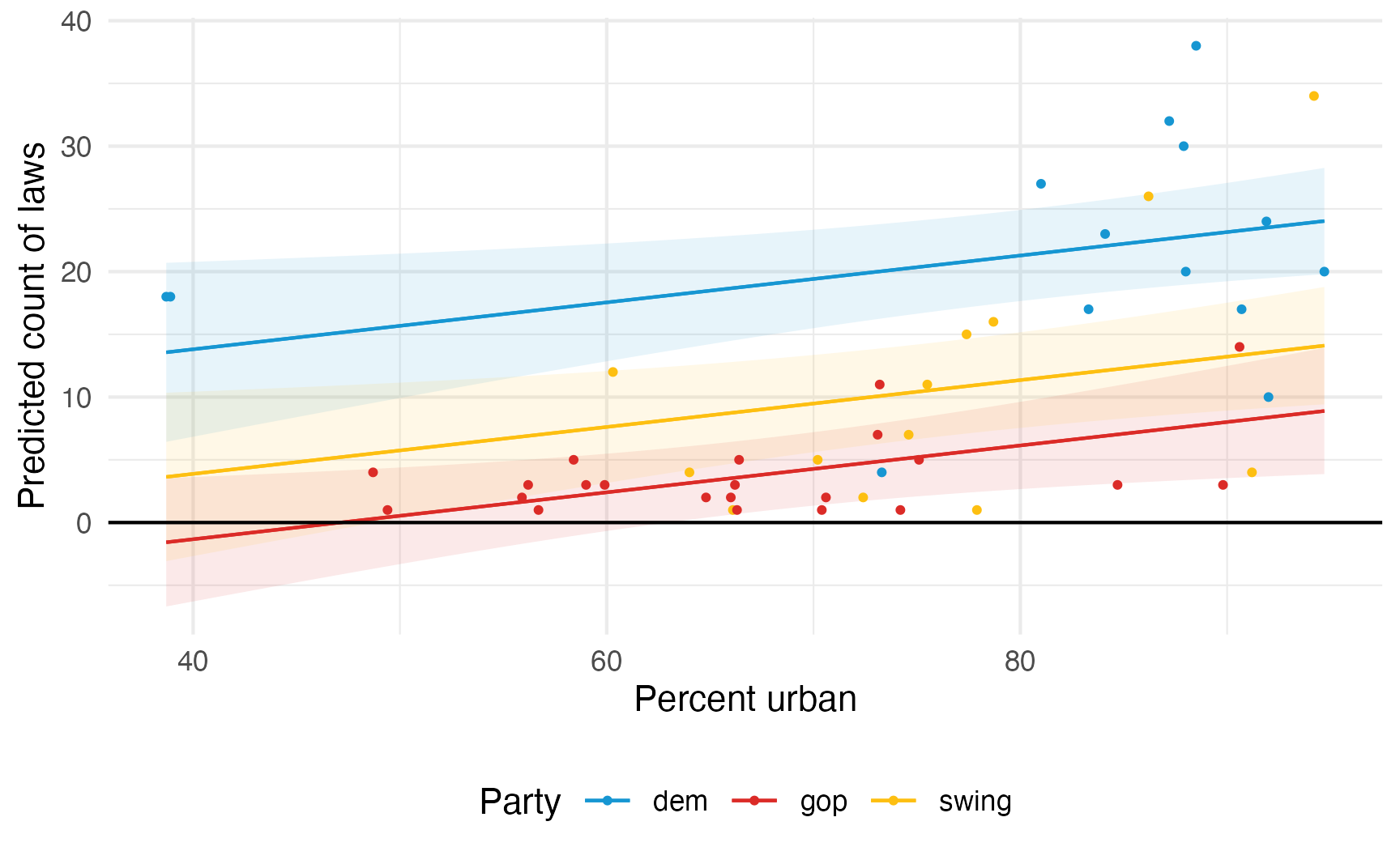
If we model it using Poisson, all the predictions are positive and the predicted lines are curvy and better fit the data:
model_poisson <- glm(
laws ~ percent_urban + historical,
data = equality,
family = poisson(link = "log")
)
plot_predictions(model_poisson, condition = c("percent_urban", "historical")) +
geom_hline(yintercept = 0) +
geom_point(
data = equality,
aes(x = percent_urban, y = laws, color = historical),
size = 0.75
) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind)) +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind), guide = "none") +
labs(
x = "Percent urban",
y = "Predicted count of laws",
color = "Party"
) +
theme(legend.position = "bottom")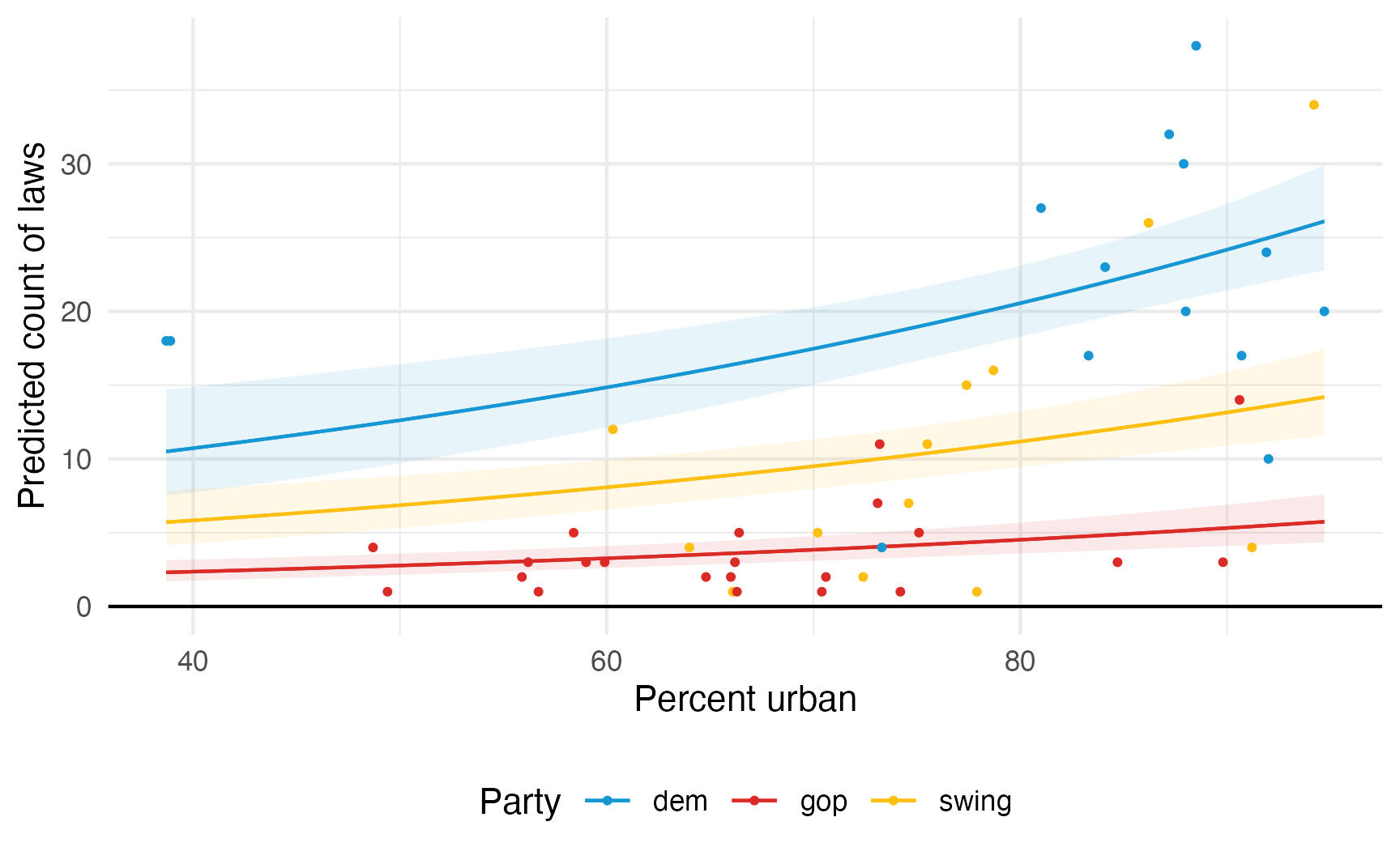
Interpreting coefficients
The coefficients in the model are on a logged scale, which make them a little weird to work with. Here’s a basic frequentist model, with coefficients logged and exponentiated:
Code
model_basic <- glm(laws ~ percent_urban + historical, data = equality,
family = poisson(link = "log"))
model_parameters(model_basic) |>
tt() |>
format_tt(j = "p", fn = scales::label_pvalue())| Parameter | Coefficient | SE | CI | CI_low | CI_high | z | df_error | p |
|---|---|---|---|---|---|---|---|---|
| (Intercept) | 1.722 | 0.3049 | 0.95 | 1.1051 | 2.301 | 5.6 | Inf | <0.001 |
| percent_urban | 0.016 | 0.0036 | 0.95 | 0.0095 | 0.023 | 4.6 | Inf | <0.001 |
| historicalgop | -1.514 | 0.1353 | 0.95 | -1.7842 | -1.253 | -11.2 | Inf | <0.001 |
| historicalswing | -0.609 | 0.1054 | 0.95 | -0.8182 | -0.405 | -5.8 | Inf | <0.001 |
Code
model_parameters(model_basic, exponentiate = TRUE) |>
tt() |>
format_tt(j = "p", fn = scales::label_pvalue())| Parameter | Coefficient | SE | CI | CI_low | CI_high | z | df_error | p |
|---|---|---|---|---|---|---|---|---|
| (Intercept) | 5.6 | 1.707 | 0.95 | 3.02 | 9.98 | 5.6 | Inf | <0.001 |
| percent_urban | 1.02 | 0.0036 | 0.95 | 1.01 | 1.02 | 4.6 | Inf | <0.001 |
| historicalgop | 0.22 | 0.0298 | 0.95 | 0.17 | 0.29 | -11.2 | Inf | <0.001 |
| historicalswing | 0.54 | 0.0573 | 0.95 | 0.44 | 0.67 | -5.8 | Inf | <0.001 |
For the intercept \(\beta_0\), this is the intercept on the logged scale when percent urban is 0 in historically Democratic states (since it’s the omitted base case). We can backtransform this to the response/count scale by exponentiating it: \(e^{1.7225} = 5.599\). That means that in a historically Democratic non-urban state, we’d expect to see 5.6 anti-discrimination laws.
But the most un-urban Democratic states are Maine and Vermont, each at 38% urban, so the intercept isn’t super important here.
For the percent urban \(\beta_1\) coefficient, this is the slope of the line on the log scale. We can expect the logged number of laws in states to increase by 0.0163 for every additional percentage point of urban-ness. To make that more interpretable we can exponentiate it (\(e^{0.0163} = 1.0164\)), which means that a 1 percentage point increase in urban-ness is associated with 1.0164 times more anti-discrimination laws (or 1.64%)
For the party/
historical\(\beta_2\) and \(\beta_3\) coefficients, these are the shifts in the logged Democratic intercept (again because it’s the omitted base case). We’d thus expect the logged number of laws in GOP states to be 1.5 lower on average. That makes no sense when logged, but if we exponentiate it (\(e^{-1.5145} = 0.2199\)), we find that GOP states should have 22% as many anti-discrimination laws as a Democratic state (or only 22% of what a typical Democratic state would have).
Even when exponentiated, these coefficients are a litte weird because they’re not on the scale of the outcome. They don’t represent changes in counts, but percent changes (e.g. increasing urbanness is associated with 1.64% more laws, not some count of laws).
To make life even easier, we can calculate marginal effects instead and get count-level changes in the outcome at specific values of urbanness or across the whole range of the fitted line.
Remember the fitted lines here—the effect or slope of urbanness changes depending on two things:
- The political party: the line is higher and steeper for democratic states
- The level of urbanness: the line is shallower in less urban states; steeper in urban states
plot_predictions(model_poisson, condition = c("percent_urban", "historical")) +
geom_vline(xintercept = c(45, 85)) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind)) +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind), guide = "none") +
labs(
x = "Percent urban",
y = "Predicted count of laws",
color = "Party"
) +
theme(legend.position = "bottom")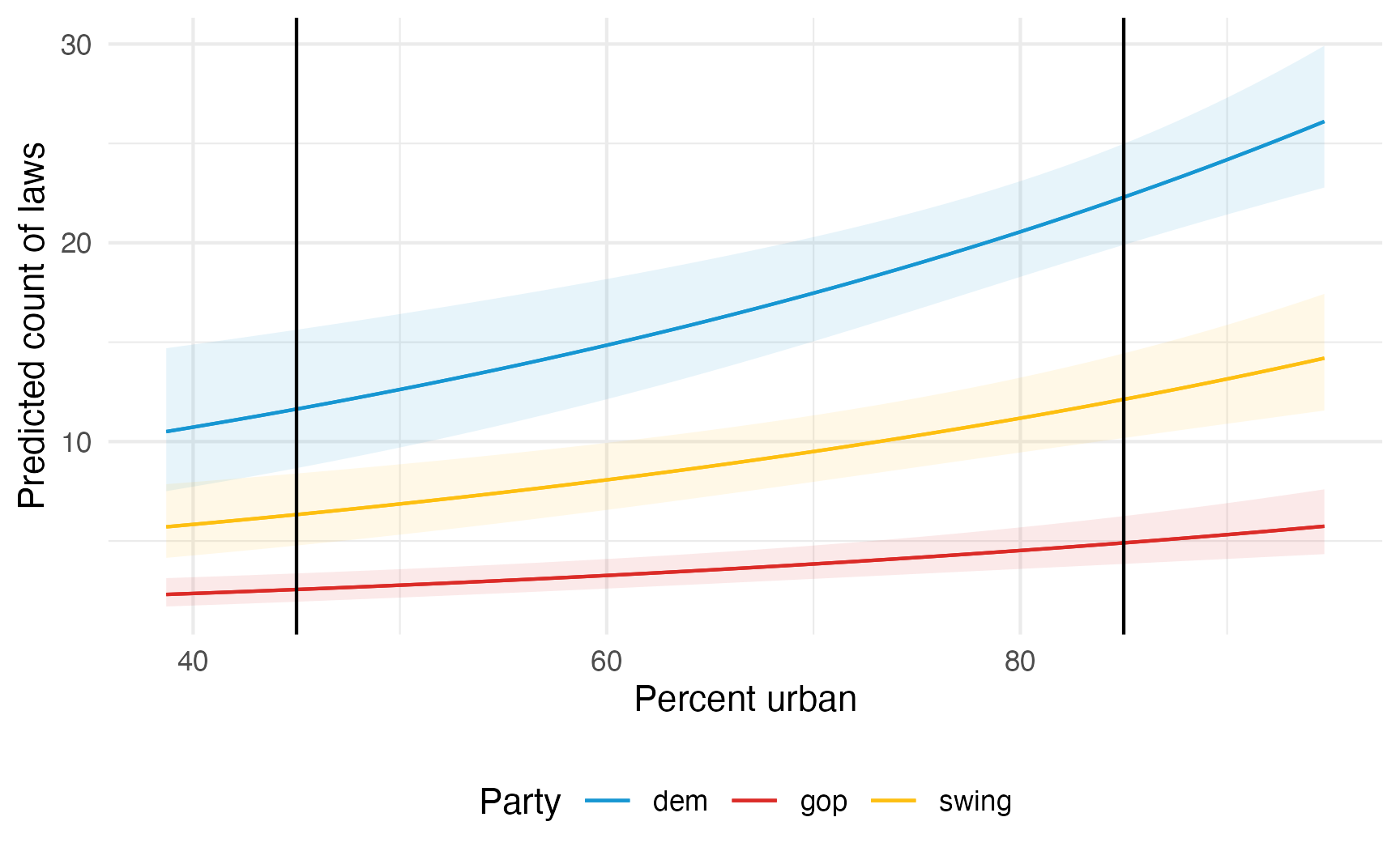
The effect of urbanness on the count of laws is different when a state is less urban (45%) vs. more urban (85%). We can calculate count-level slopes at each of those points:
model_poisson |>
slopes(
newdata = datagrid(percent_urban = c(45, 85), historical = unique),
variables = "percent_urban"
)
##
## Term percent_urban historical Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
## percent_urban 45 gop 0.0416 0.00719 5.78 <0.001 27.0 0.0275 0.0557
## percent_urban 45 swing 0.1029 0.01375 7.48 <0.001 43.6 0.0759 0.1298
## percent_urban 45 dem 0.1892 0.01876 10.08 <0.001 77.0 0.1524 0.2259
## percent_urban 85 gop 0.0797 0.02367 3.37 <0.001 10.4 0.0333 0.1261
## percent_urban 85 swing 0.1971 0.05126 3.85 <0.001 13.0 0.0967 0.2976
## percent_urban 85 dem 0.3625 0.08355 4.34 <0.001 16.1 0.1987 0.5262
##
## Type: response
## Columns: rowid, term, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, percent_urban, historical, predicted_lo, predicted_hi, predicted, lawsIn Democratic states, a 1 percentage point increase in urbanness is associated with 0.189 additional laws in rural (45%) states and 0.363 additional laws in urban (85%) states; in Republican states, a 1 percentage point increase in urbanness is associated with 0.04 additional laws in rural (45%) states and 0.08 ladditional laws in urban (85%) states.
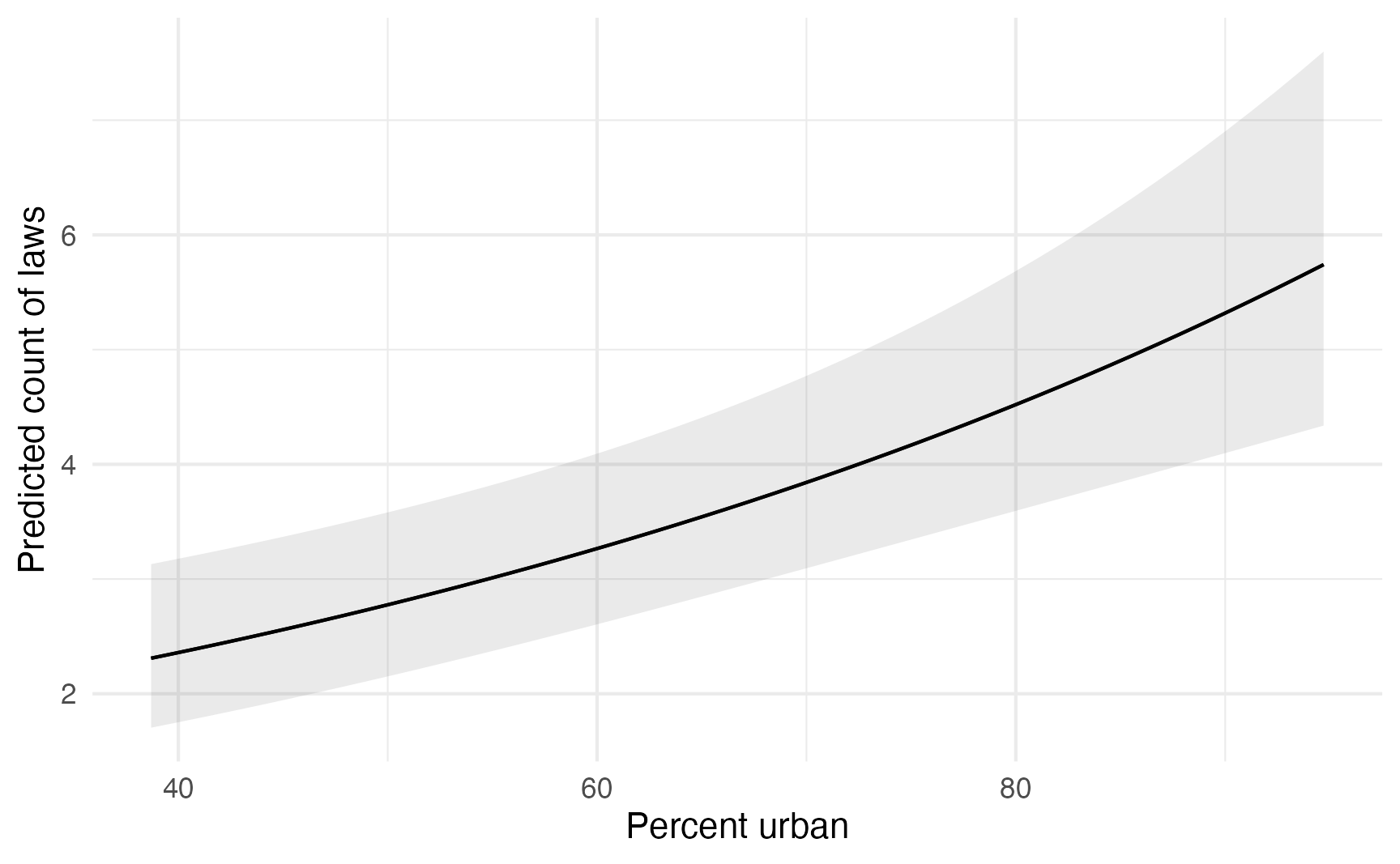
Instead of disaggregating everything by party and choosing arbitrary values of urbanness, we can also find the overall average slope of the line. Across all states and parties and different levels of urbanness, a 1 percentage point increase in urbanness is associated with 0.17 additional laws, on average.
model_poisson |>
avg_slopes(variables = "percent_urban")
##
## Estimate Std. Error z Pr(>|z|) S 2.5 % 97.5 %
## 0.172 0.0385 4.47 <0.001 17.0 0.0965 0.247
##
## Term: percent_urban
## Type: response
## Comparison: mean(dY/dX)
## Columns: term, contrast, estimate, std.error, statistic, p.value, s.value, conf.low, conf.high, predicted_lo, predicted_hi, predicted
model_poisson |>
plot_predictions(condition = "percent_urban") +
labs(
x = "Percent urban",
y = "Predicted count of laws"
)
Bayesian Poisson models
We can run this model with Bayesian regression too. We’ll set some weakly informative priors and define the model like this:
\[ \begin{aligned} \text{Laws}_i &\sim \operatorname{Poisson}(\lambda_i) \\ \log(\lambda_i) &= \beta_0 + \beta_1\ \text{Percent urban}_i + \beta_2\ \text{GOP}_i + \beta_3\ \text{Swing}_i \\ \\ \beta_0 &\sim \mathcal{N}(0, 2) \\ \beta_{1 \dots 3} &\sim \operatorname{Student t}(\nu = 3, \mu = 0, \sigma = 1) \end{aligned} \]
Here’s what those priors look like:
priors <- c(
prior(normal(0, 2), class = Intercept),
prior(student_t(3, 0, 1), class = b)
)
priors |>
parse_dist() |>
ggplot(aes(y = 0, dist = .dist, args = .args, fill = prior)) +
stat_slab(normalize = "panels") +
scale_fill_viridis_d(option = "plasma", begin = 0.2, end = 0.8) +
facet_wrap(vars(prior), scales = "free_x")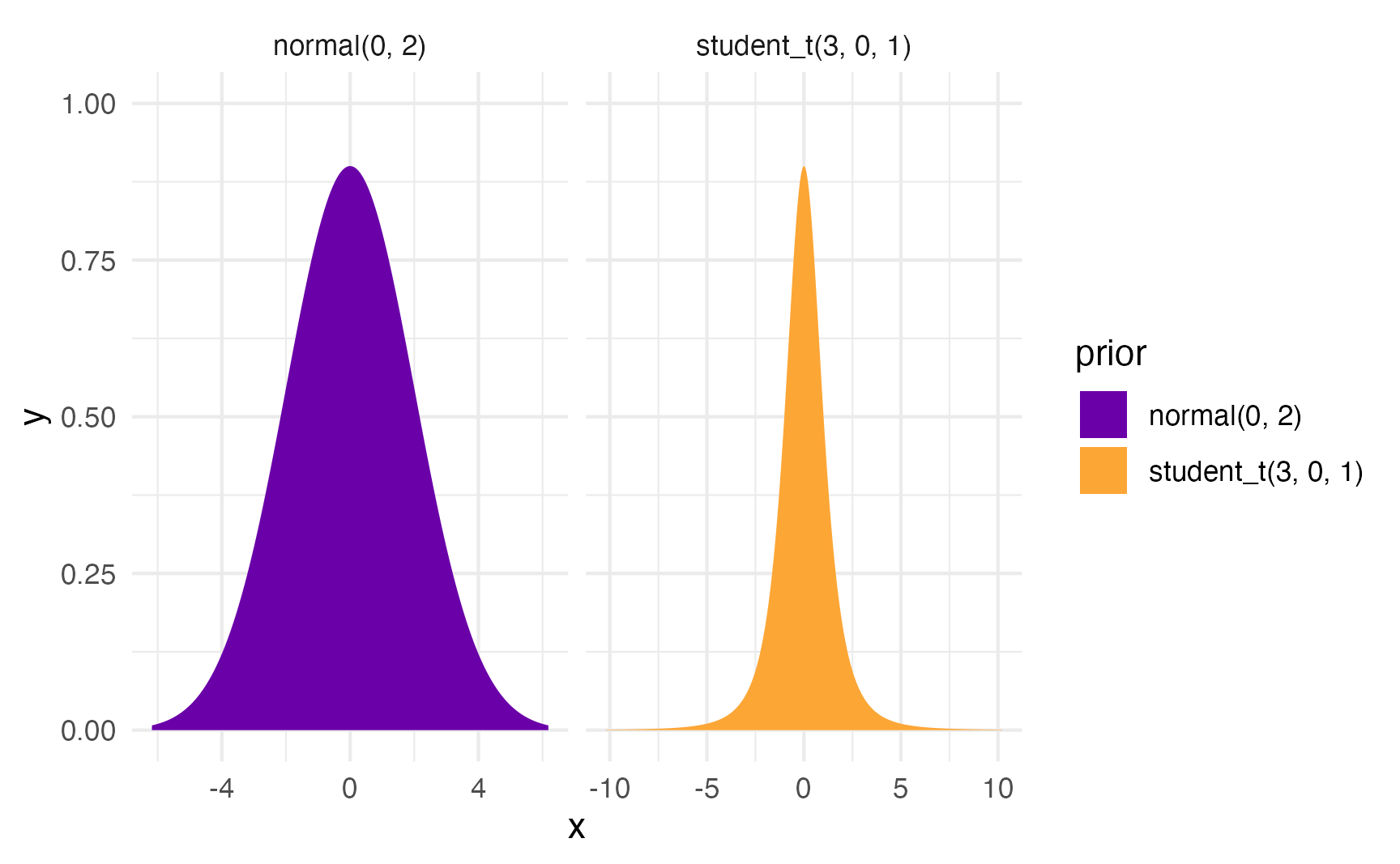
And here’s the model:
Code
model_poisson_bayes <- brm(
bf(laws ~ percent_urban + historical),
data = equality,
family = poisson(),
prior = priors,
chains = 4, iter = 2000, seed = 1234,
file = "models/model_poisson_bayes"
)Code
model_parameters(model_poisson_bayes, verbose = FALSE) |> tt()| Parameter | Median | CI | CI_low | CI_high | pd | Rhat | ESS |
|---|---|---|---|---|---|---|---|
| b_Intercept | 1.679 | 0.95 | 1.0773 | 2.253 | 1 | 1 | 3372 |
| b_percent_urban | 0.017 | 0.95 | 0.0099 | 0.024 | 1 | 1 | 3707 |
| b_historicalgop | -1.497 | 0.95 | -1.7621 | -1.239 | 1 | 1 | 2228 |
| b_historicalswing | -0.598 | 0.95 | -0.8005 | -0.391 | 1 | 1 | 2642 |
We can visualize the posterior distribution for each coefficient:
model_poisson_bayes |>
gather_draws(`^b_.*`, regex = TRUE) |>
mutate(.value = exp(.value)) |>
mutate(.variable = factor(.variable,
levels = c("b_Intercept", "b_percent_urban",
"b_historicalgop", "b_historicalswing"),
ordered = TRUE)) |>
ggplot(aes(x = .value, fill = .variable)) +
stat_halfeye(normalize = "xy") +
scale_fill_viridis_d(option = "plasma", begin = 0.1, end = 0.9, guide = "none") +
labs(x = "Coefficient value", y = NULL) +
facet_wrap(vars(.variable), scales = "free_x") +
theme(axis.text.y = element_blank())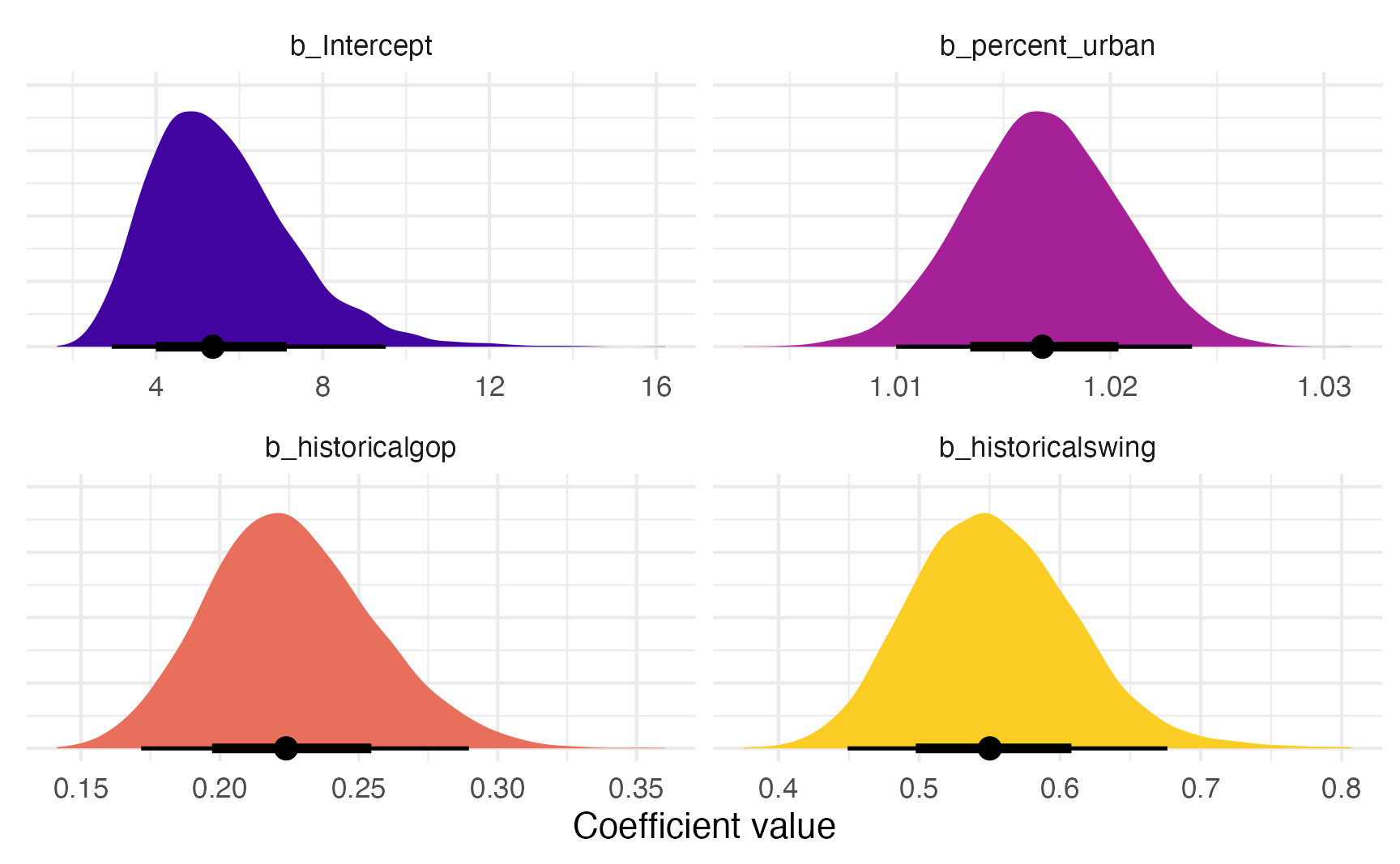
And we can see posterior predictions, either manually with {tidybayes}…
equality |>
add_epred_draws(model_poisson_bayes, ndraws = 50) |>
ggplot(aes(x = percent_urban, y = laws, color = historical)) +
geom_point(data = equality, size = 1) +
geom_line(aes(y = .epred, group = paste(historical, .draw)),
linewidth = 0.5, alpha = 0.3) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind))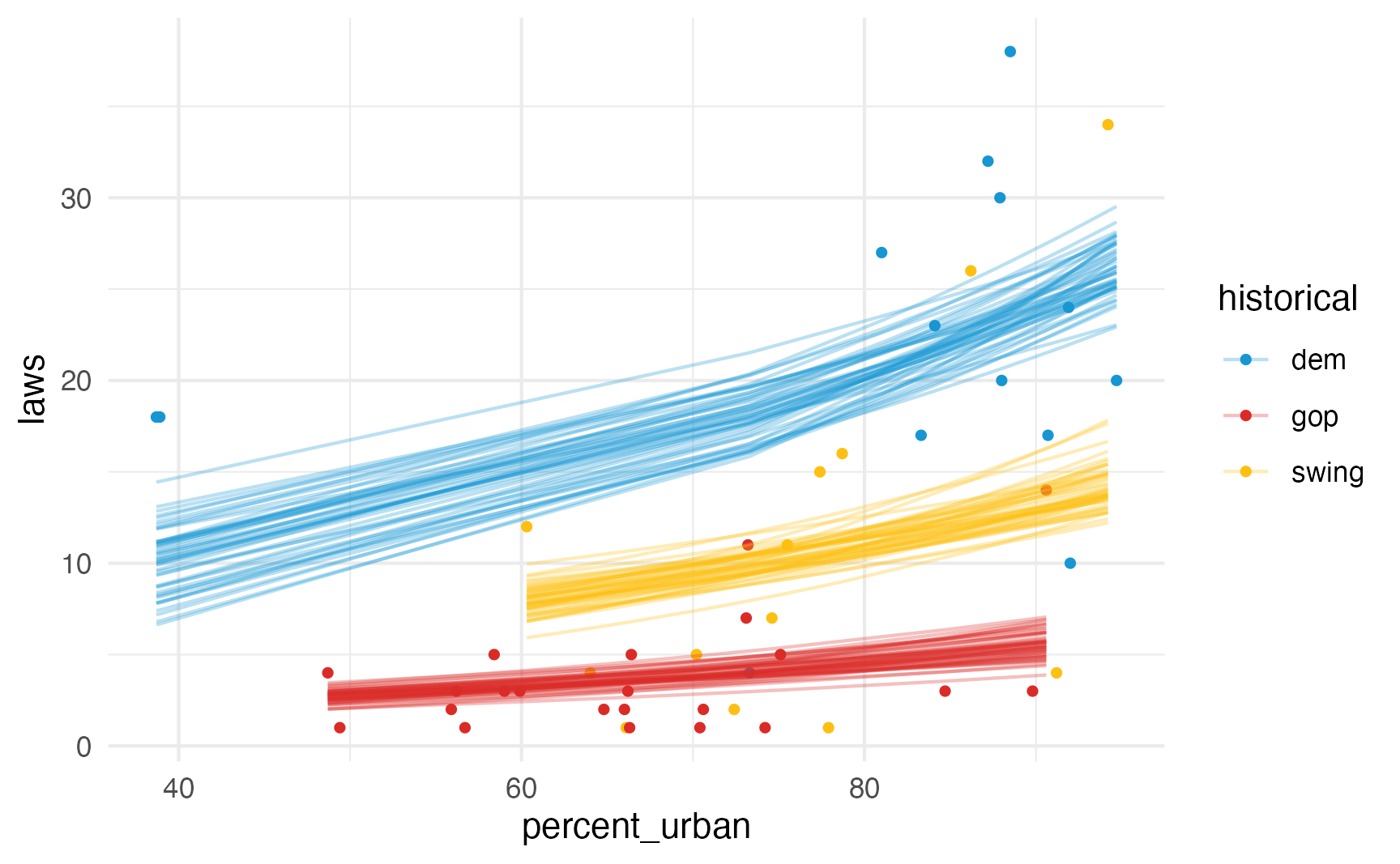
…or more automatically with {marignaleffects}:
model_poisson_bayes |>
plot_predictions(condition = c("percent_urban", "historical")) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind)) +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind), guide = "none") +
labs(
x = "Percent urban",
y = "Predicted count of laws",
color = "Party"
) +
theme(legend.position = "bottom")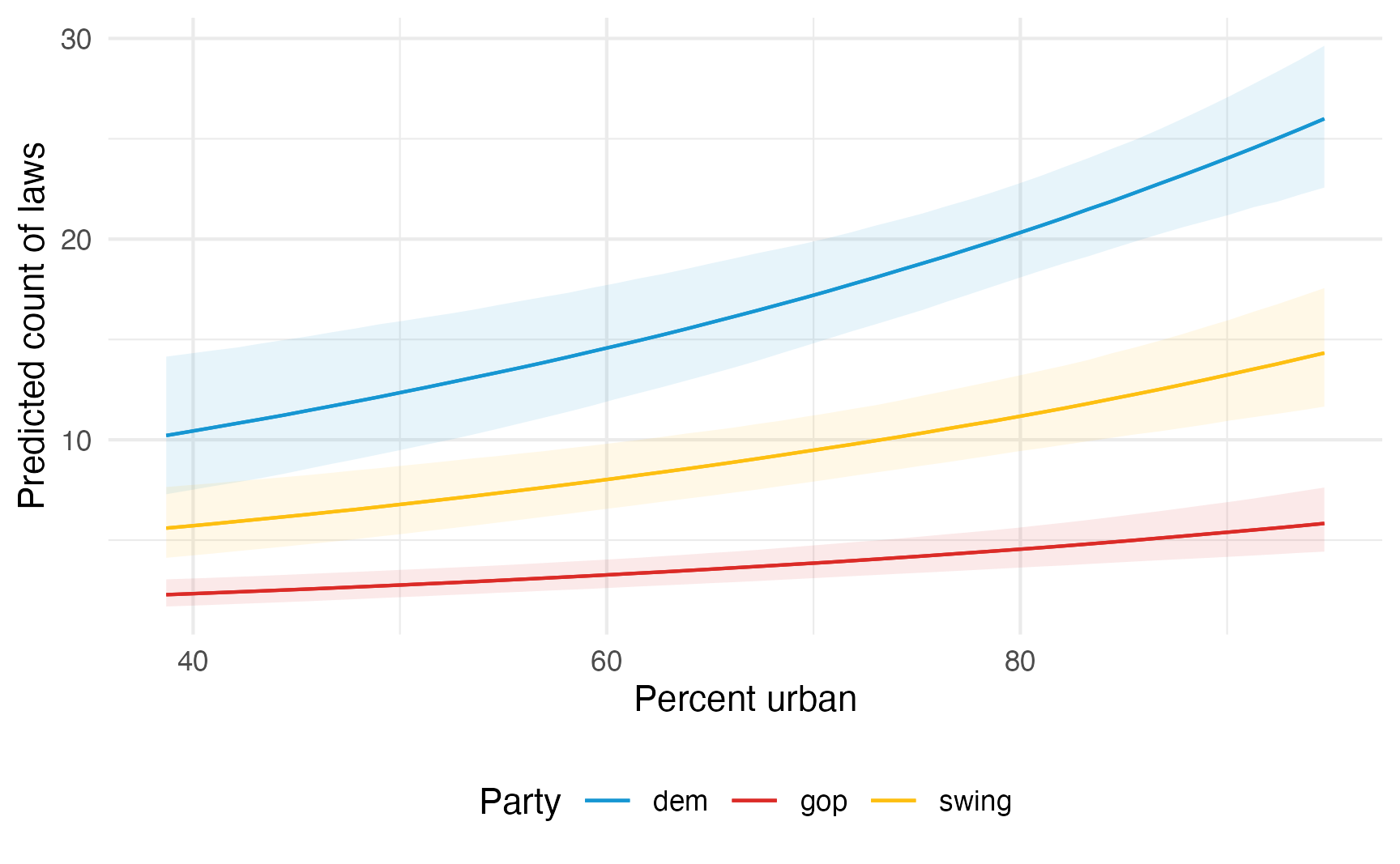
…or as a fancy spaghetti plot with {marginaleffects}:
model_poisson_bayes |>
predictions(condition = c("percent_urban", "historical"), ndraws = 50) |>
posterior_draws() |>
ggplot(aes(x = percent_urban, y = draw, color = historical)) +
geom_line(aes(y = draw, group = paste(historical, drawid)),
size = 0.5, alpha = 0.3) +
scale_color_manual(values = c(clr_dem, clr_gop, clr_ind)) +
labs(
x = "Percent urban",
y = "Predicted count of laws",
color = "Party"
) +
theme(legend.position = "bottom")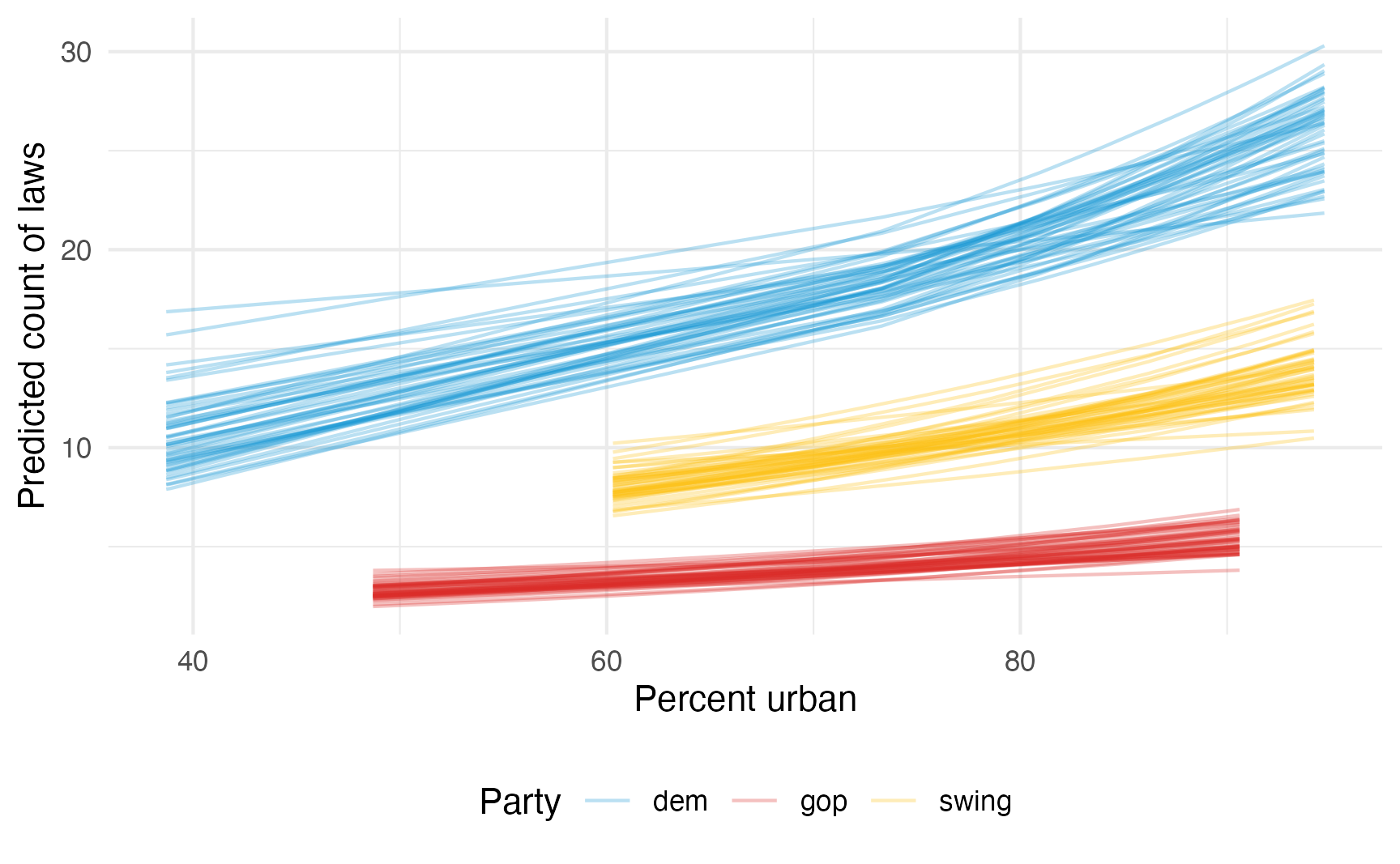
We can interpret the coefficients using marginal effects too. By themselves, we see posterior medians:
model_poisson_bayes |>
slopes(
newdata = datagrid(percent_urban = c(45, 85), historical = unique),
variables = "percent_urban"
)
##
## Term percent_urban historical Estimate 2.5 % 97.5 %
## percent_urban 45 gop 0.0421 0.0279 0.0558
## percent_urban 45 swing 0.1034 0.0738 0.1291
## percent_urban 45 dem 0.1877 0.1417 0.2183
## percent_urban 85 gop 0.0826 0.0420 0.1371
## percent_urban 85 swing 0.2021 0.1110 0.3136
## percent_urban 85 dem 0.3688 0.2132 0.5319
##
## Type: response
## Columns: rowid, term, estimate, conf.low, conf.high, percent_urban, historical, predicted_lo, predicted_hi, predicted, tmp_idx, lawsWe can also visualize the posterior distributions of the specific marginal effects:
model_poisson_bayes |>
slopes(
newdata = datagrid(percent_urban = c(45, 85), historical = unique),
variables = "percent_urban"
) |>
posterior_draws() |>
ggplot(aes(x = draw, y = factor(percent_urban), fill = historical)) +
stat_halfeye(normalize = "panels") +
scale_fill_manual(values = c(clr_dem, clr_gop, clr_ind), guide = "none") +
facet_wrap(vars(historical), ncol = 1) +
labs(x = "Additional laws", y = "Percent urban")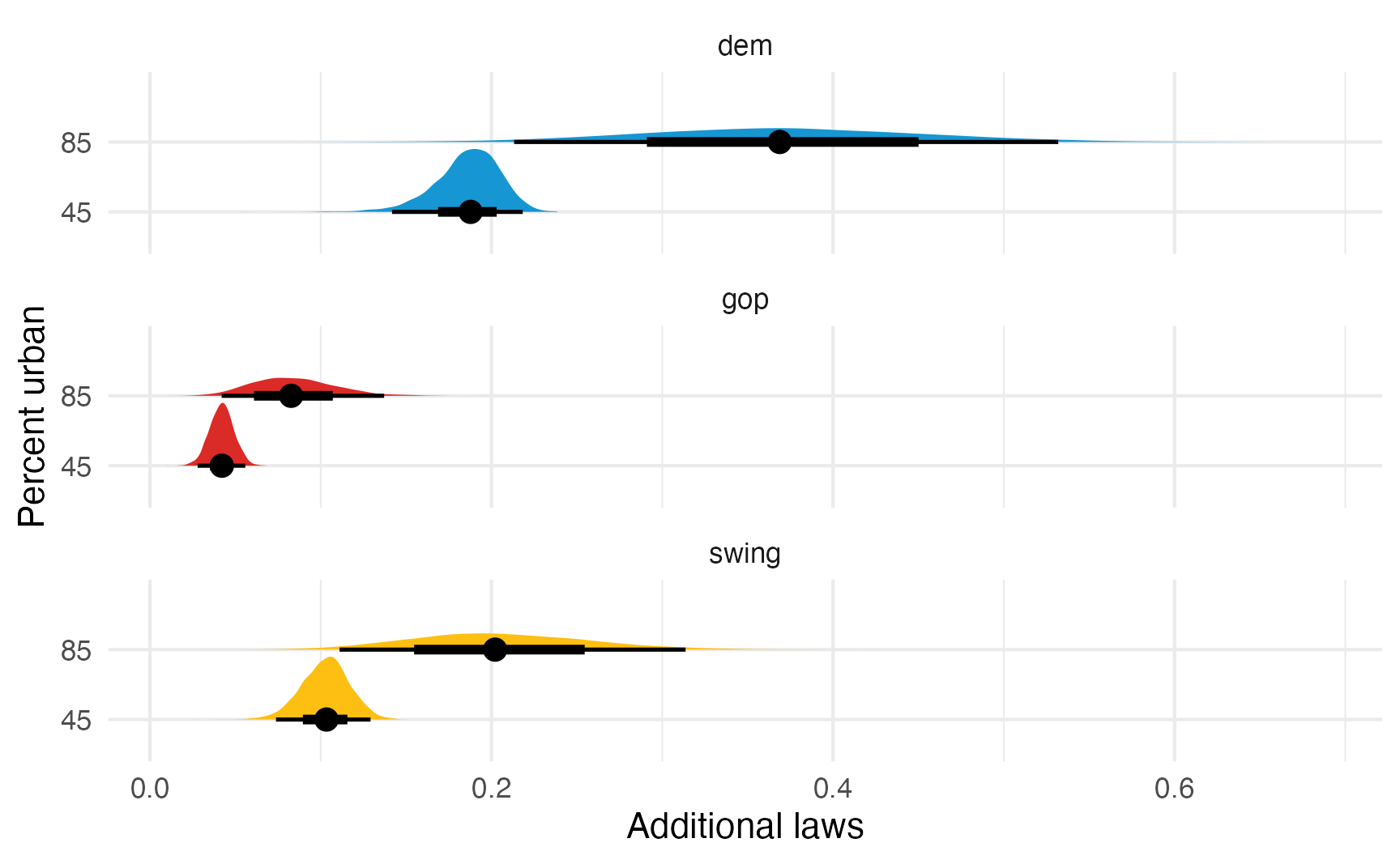
Negative binomial regression
Recall that Poisson distributions assume that the mean and variance of the outcome are the same. If that’s not the cause, you can still run a model! You just have to work with two parameters:
- \(\mu\) (mu) for the mean
- \(r\) for the dispersion
You can do this with Stan and {brms} (see section 12.6 of Bayes Rules! for an example). Like we did with regular normal/gaussian regresison, you can specify an overall \(r\) value, or a specific separate model for it \(r\):
Same overall \(r\):
\[ \begin{aligned} Y_u &\sim \operatorname{NegBin}(\mu_i, r) \\ \log(\mu_i) &= \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots \\ \\ \beta_0, \beta_1, \beta_2, \beta_{\dots} &\sim \text{Some prior} \\ r &\sim \text{Some prior} > 0 \end{aligned} \]
\(r\) specific model
\[ \begin{aligned} Y_u &\sim \operatorname{NegBin}(\mu_i, r_i) \\ \log(\mu_i) &= \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots \\ \log(\mu_i) &= \gamma_0 + \gamma_1 X_{i1} + \gamma_2 X_{i2} + \dots \\ \\ \beta_0, \beta_1, \beta_2, \beta_{\dots} &\sim \text{Some prior} \\ \gamma_0, \gamma_1, \gamma_2, \gamma_{\dots} &\sim \text{Some prior} \end{aligned} \]
Here’s what that might look like with {brms}
model_negbinom <- brm(
bf(
laws ~ percent_urban + historical,
shape ~ percent_urban + historical),
data = equality,
family = negbinomial(),
...
)