Beta regression

library(tidyverse)
library(marginaleffects)
library(brms)
library(tidybayes)
library(parameters)
library(tinytable)
library(patchwork)
library(extraDistr)
library(ggridges)
library(scales)
library(betareg)

# Data via the WHO via Kaggle
# https://www.kaggle.com/datasets/lsind18/who-immunization-coverage
tetanus <- readRDS("data/data-processed/tetanus_pab.rds")
tetanus_2010 <- tetanus |> 
  filter(year == 2010) |> 
  # Cheat a little
  mutate(prop_pab = ifelse(prop_pab == 1, 0.999, prop_pab))

theme_set(theme_minimal())

options(mc.cores = 4)  # Use 4 cores for {brms}

Recall that the Beta distribution captures values between 0 and 1 (but not including 0 and 1), which makes it great for outcomes like proportions.

We can use regression to model the $\mu$ (mu) and $\phi$ (phi) parameters of a Beta-distributed outcome. The neat thing about distributional regression like this is that we can model both parameters independently if we want—if we think there’s a reason that precision/spread of the distribution differs across different values of explanatory variables, we can incorporate that! We can also just model the $\mu$ part and leave $\phi$ constant.

To make sure the $\mu$ and $\phi$ parameters stay positive, we use a logit link function for $\mu$ and a log link function for $\phi$. Here I use $\gamma$ (gamma) for the $\phi$ coefficients just to show that it’s a different model, but the Xs can be the same:

\[ \begin{aligned} \operatorname{logit}(\mu_i) &= \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots \\ \log(\phi_i) &= \gamma_0 + \gamma_1 X_{i1} + \gamma_2 X_{i2} + \dots \\ \end{aligned} \]

In general, the model looks like this:

\[ \begin{aligned} Y_i &\sim \operatorname{Beta}(\mu_i, \phi_i) \\ \operatorname{logit}(\mu_i) &= \beta_0 + \beta \mathbf{X}_i \\ \log(\phi_i) &= \gamma_0 + \gamma \mathbf{X}_i \end{aligned} \]

Example: Modeling the proprotion of tetanus vaccinations

We want to model the proportion of 1-year-olds who are vaccinated against tetanus through maternal vaccination, or protection at birth (PAB) vaccination. This vaccination was introduced in the 1980s and slowly rolled out globally, so that in 2020, more than 80% of the world’s infants are pre-vaccinated against tetanus.

tetanus |> 
  ggplot(aes(x = prop_pab, y = factor(year), fill = after_stat(x))) +
  geom_density_ridges_gradient(quantile_lines = TRUE, quantiles = 2, color = "white") +
  scale_x_continuous(labels = label_percent()) +
  scale_fill_viridis_c(option = "plasma", guide = "none") +
  labs(x = "Proportion of PAB vaccination", y = NULL) +
  theme(panel.grid.major.y = element_blank())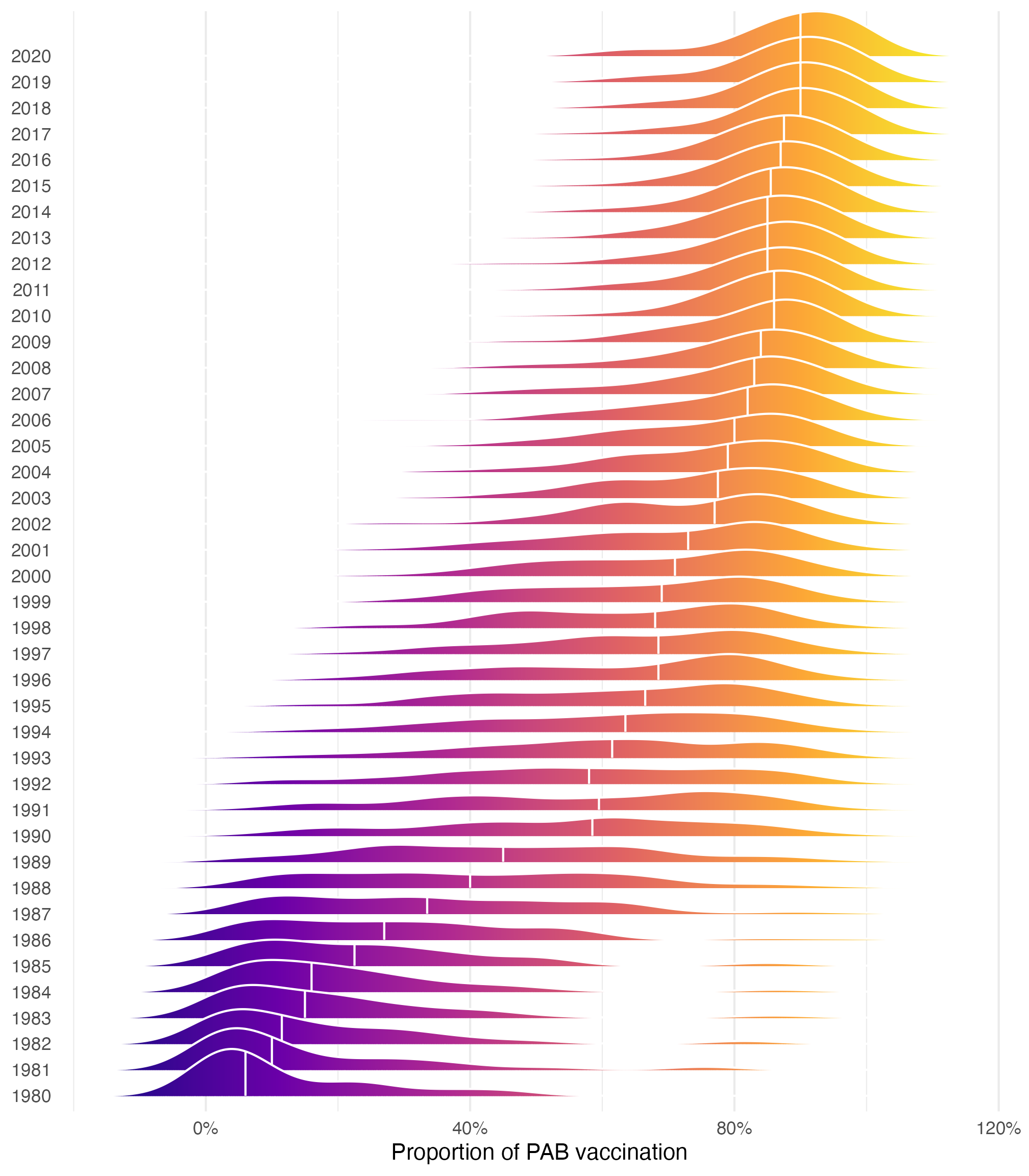

We have complex panel data for all countries across 1980-2020, and we could model that time structure with multilevel models, but for the sake of simplicity, we’ll just look at one year (I chose 2010 arbitrarily):

ggplot(tetanus_2010, aes(x = prop_pab)) +
  geom_density(fill = "darkorange", color = NA) +
  scale_x_continuous(labels = label_percent()) +
  labs(title = "PAB proportion in 2010", x = "Proportion of PAB vaccination", y = NULL) +
  theme(
    panel.grid.major.y = element_blank(),
    axis.text.y = element_blank()
  )

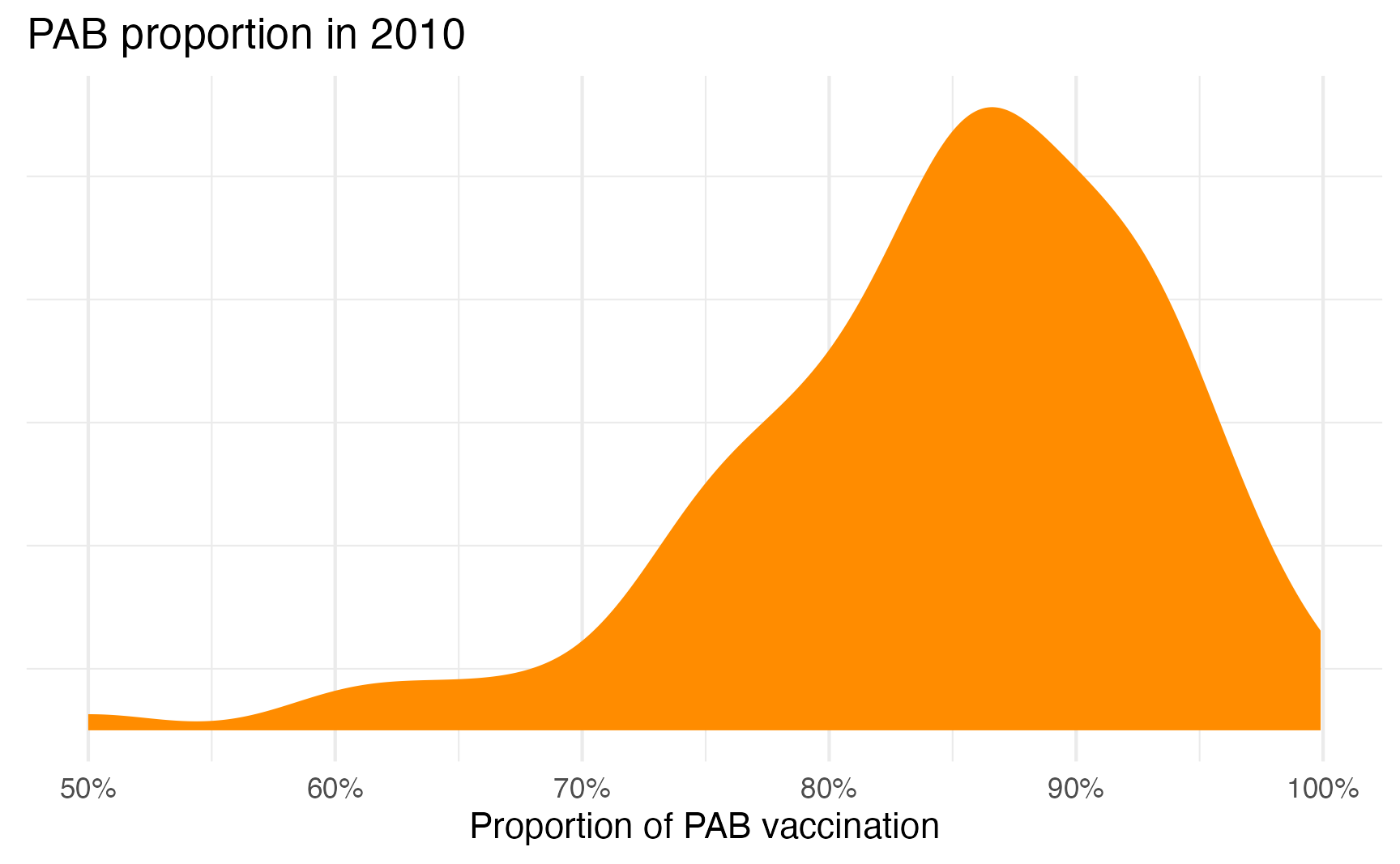
That feels very Beta-y and seems to be clustered around 85%ish. We can actually find its emperical mean and precision by fitting an intercept-only model:

model_int_only <- betareg(prop_pab ~ 1, data = tetanus_2010)
model_int_only
## 
## Call:
## betareg(formula = prop_pab ~ 1, data = tetanus_2010)
## 
## Coefficients (mean model with logit link):
## (Intercept)  
##        1.72  
## 
## Phi coefficients (precision model with identity link):
## (phi)  
##  14.4

The $\mu$ is 1.72, but on the logit scale. We can back-transform it to real numbers with plogis(1.72), or 0.848. The $\phi$ is 14.4.

In $a$ and $b$ terms, here are the shapes:

muphi_to_shapes <- function(mu, phi) {
  shape1 <- mu * phi
  shape2 <- (1 - mu) * phi
  return(list(shape1 = shape1, shape2 = shape2))
}

muphi_to_shapes(plogis(1.72), 14.4)
## $shape1
## [1] 12.2
## 
## $shape2
## [1] 2.19

That means our shape-based fraction is:

\[ \frac{12.2}{12.2 + 2.19} = \frac{12.2}{14.39} \]

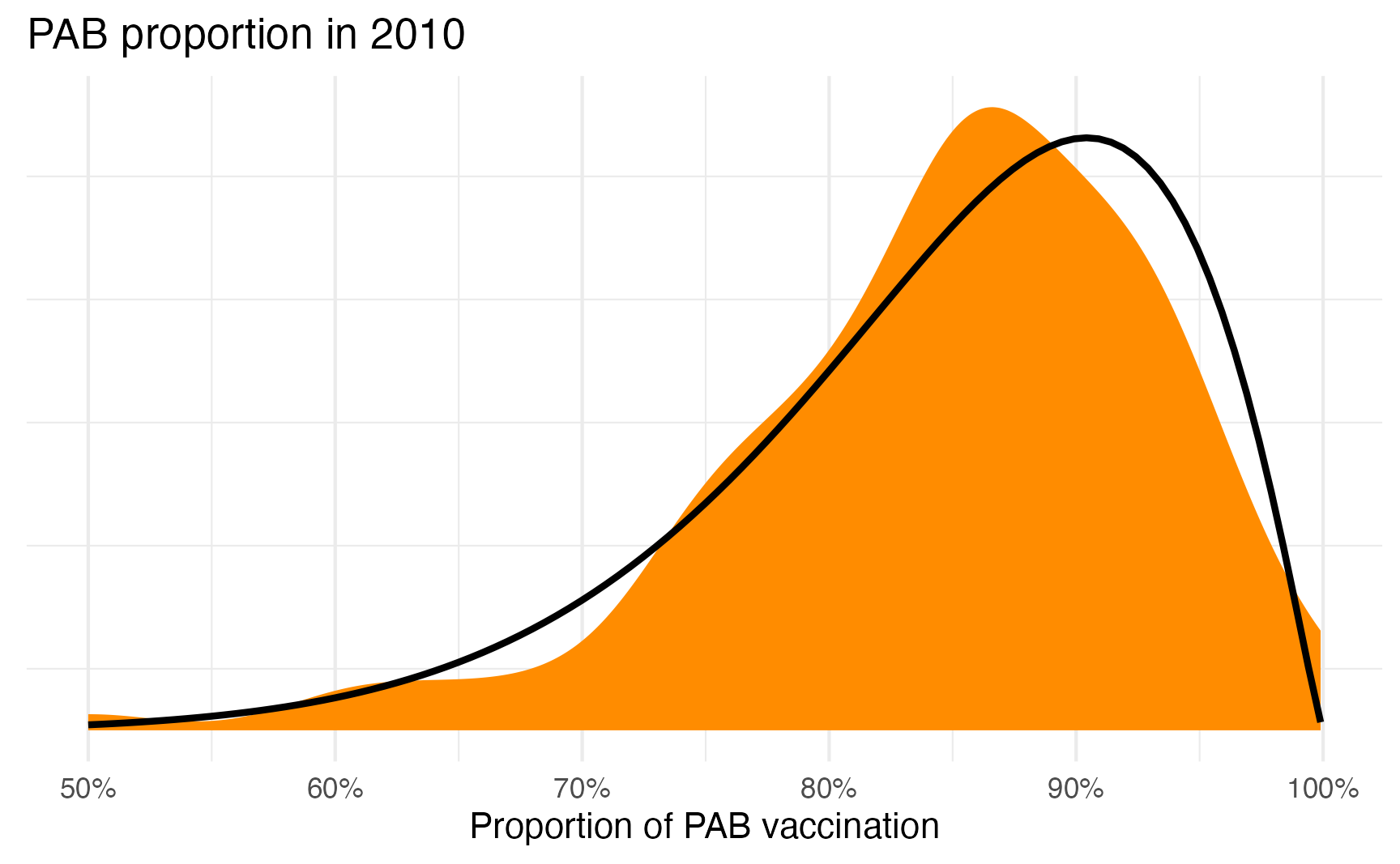
And here’s what it looks like overlaid on the actual distribution. Not perfect, but pretty close!

ggplot(tetanus_2010, aes(x = prop_pab)) +
  geom_density(fill = "darkorange", color = NA) +
  geom_function(fun = dprop, args = list(mean = plogis(1.72), size = 14.4),
                linewidth = 1) +
  scale_x_continuous(labels = label_percent()) +
  labs(title = "PAB proportion in 2010", x = "Proportion of PAB vaccination", y = NULL) +
  theme(
    panel.grid.major.y = element_blank(),
    axis.text.y = element_blank()
  )

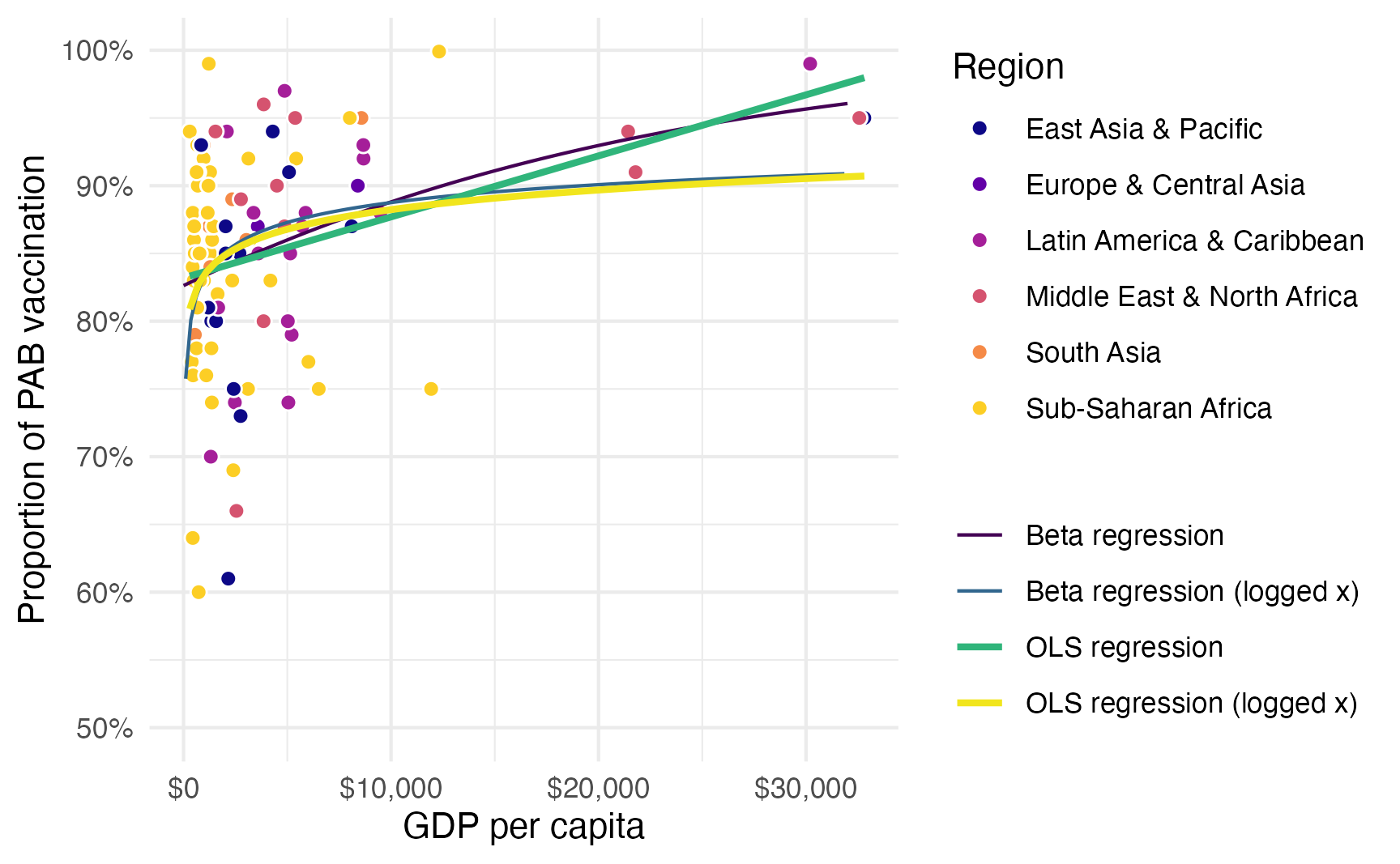
We want to model the proportion of vaccinated infants based on a country’s GDP per capita and its region. Here’s the general relationship. A regular straight OLS line doesn’t fit the data well because GDP per capita is so skewed. We can log GDP per capita, and that helps, but it underpredicts countries with high GDP per capita. Beta regression fits a lot better and captures the outcome.

beta_line <- predictions(
  model = betareg(prop_pab ~ gdp_per_cap, data = tetanus_2010), 
  newdata = datagrid(gdp_per_cap = seq(0, 32000, by = 250))
)

beta_log_line <- predictions(
  model = betareg(prop_pab ~ log(gdp_per_cap), data = tetanus_2010), 
  newdata = datagrid(gdp_per_cap = seq(100, 32000, by = 250))
)

ggplot(tetanus_2010, aes(x = gdp_per_cap, y = prop_pab)) +
  geom_point(aes(fill = region), pch = 21, size = 2, color = "white") +
  geom_line(data = beta_line, aes(y = estimate, color = "Beta regression")) +
  geom_line(data = beta_log_line, aes(y = estimate, color = "Beta regression (logged x)")) +
  geom_smooth(
    aes(color = "OLS regression"), 
    se = FALSE, method = "lm", formula = y ~ x
  ) +
  geom_smooth(
    aes(color = "OLS regression (logged x)"), 
    se = FALSE, method = "lm", formula = y ~ log(x)
  ) +
  scale_fill_viridis_d(option = "plasma", end = 0.9) +
  scale_color_viridis_d(option = "viridis", end = 0.98) +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

# The formula after the | is for the phi parameter
model_beta <- betareg(
  prop_pab ~ gdp_per_cap + region | 1, 
  data = tetanus_2010,
  link = "logit"
)

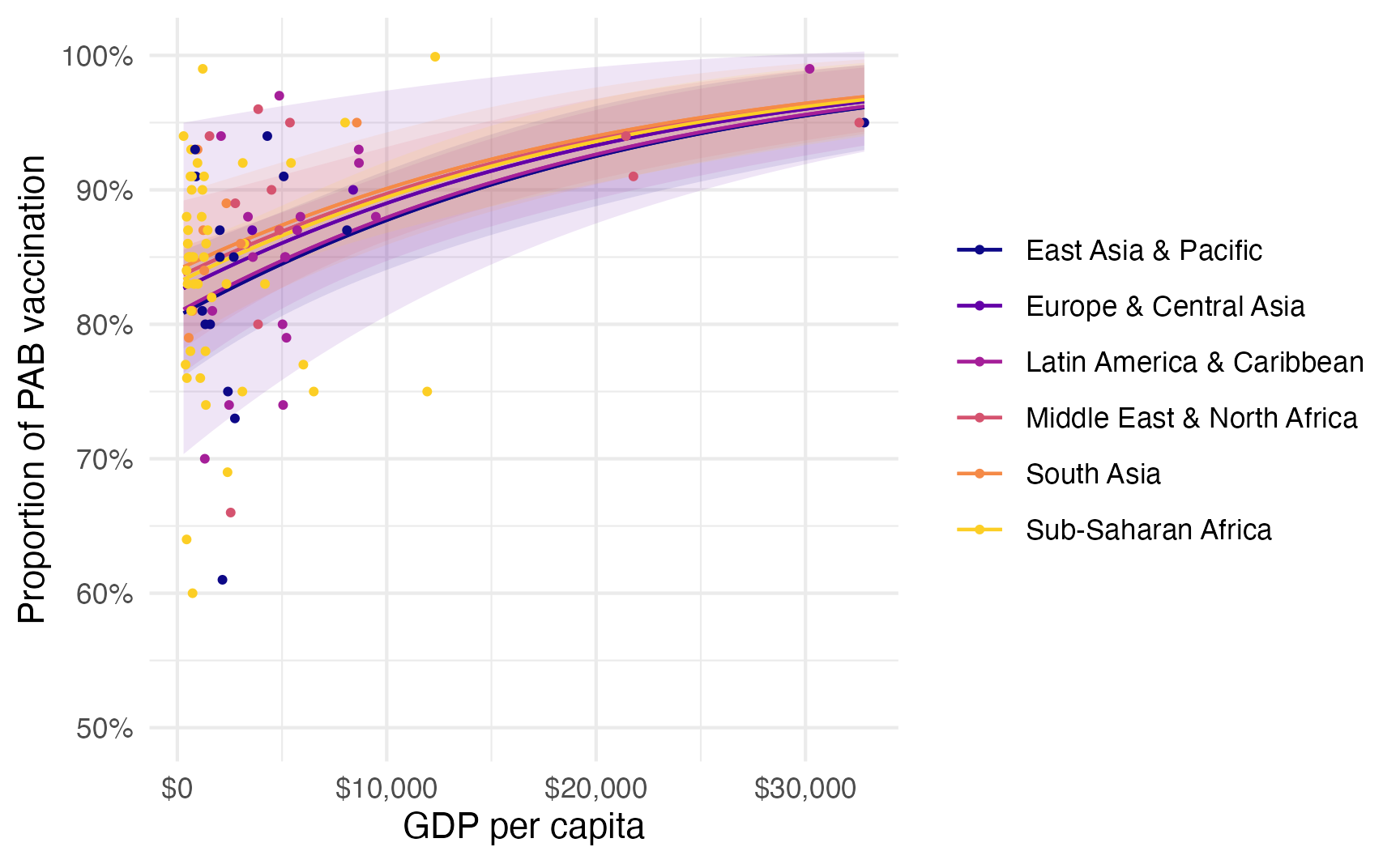
plot_predictions(model_beta, condition = c("gdp_per_cap", "region")) +
  geom_point(
    data = tetanus_2010, 
    aes(x = gdp_per_cap, y = prop_pab, color = region),
    size = 0.75
  ) +
  scale_color_viridis_d(option = "plasma", end = 0.9) +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

Interpreting coefficients

The coefficients in the model are on the logit scale, which make them a little weird to work with. Here’s a basic frequentist model, with coefficients logged and exponentiated:

Code

model_beta <- betareg(
  prop_pab ~ gdp_per_cap + region | 1,
  # prop_pab ~ I(gdp_per_cap / 1000) + region | 1,
  data = tetanus_2010,
  link = "logit"
)

model_parameters(model_beta) |> 
  tt(digits = 2) |> 
  format_tt(j = "p", fn = scales::label_pvalue())

Parameter	Coefficient	SE	CI	CI_low	CI_high	z	df_error	p
(Intercept)	1.422907	0.155966	0.95	1.11722	1.728594	9.12	Inf	<0.001
gdp_per_cap	0.000055	0.000014	0.95	0.000028	0.000082	3.96	Inf	<0.001
regionEurope & Central Asia	0.123089	0.457848	0.95	-0.774276	1.020454	0.27	Inf	0.788
regionLatin America & Caribbean	0.018405	0.205338	0.95	-0.384049	0.42086	0.09	Inf	0.929
regionMiddle East & North Africa	0.197393	0.241179	0.95	-0.275309	0.670096	0.82	Inf	0.413
regionSouth Asia	0.239095	0.258459	0.95	-0.267475	0.745666	0.93	Inf	0.355
regionSub-Saharan Africa	0.169972	0.17218	0.95	-0.167493	0.507438	0.99	Inf	0.324

Code


model_parameters(model_beta, exponentiate = TRUE) |> 
  tt(digits = 2) |> 
  format_tt(j = "p", fn = scales::label_pvalue())

Parameter	Coefficient	SE	CI	CI_low	CI_high	z	df_error	p
(Intercept)	4.1	0.647127	0.95	3.06	5.6	9.12	Inf	<0.001
gdp_per_cap	1	0.000014	0.95	1	1	3.96	Inf	<0.001
regionEurope & Central Asia	1.1	0.517819	0.95	0.46	2.8	0.27	Inf	0.788
regionLatin America & Caribbean	1	0.209152	0.95	0.68	1.5	0.09	Inf	0.929
regionMiddle East & North Africa	1.2	0.29381	0.95	0.76	2	0.82	Inf	0.413
regionSouth Asia	1.3	0.328269	0.95	0.77	2.1	0.93	Inf	0.355
regionSub-Saharan Africa	1.2	0.20408	0.95	0.85	1.7	0.99	Inf	0.324

For the intercept $\beta_0$, this is the intercept on the logit scale when GDP per capita is 0 in East Asia and the Pacific (since it’s the omitted base case). We can backtransform this to a proportion by inverse logit-ing: plogis(1.430548): 0.807. That means that in an East Asian country with no economy whatsoever, we’d expect that 80%ish of 1-year-olds would be vaccinated.
For the GDP per capita $\beta_1$ coefficient, this is the slope of the line on the logit scale. We can expect the logged odds of vaccination to increase by 0.000053 for every \$1 increase in GDP per capita. That’s tiny, so we can think of \$1,000 increases instead. Boosting GDP per capita by $1,000 increases the logged odds of vaccination by 0.053. Whatever that means.

We can also exponentiate that ($e^{0.000053 \times 1000} = 1.05$) to get an odds ratio, which means that a $1,000 increase in GDP per capita is associated with a 5% increase in vaccination rates (though not a 5 percentage point increase).
For the region coefficients, these are the shifts in the logit-scale East Asia and Pacific intercept (again because it’s the omitted base case). We’d thus expect the proportion of vaccinations to be plogis(1.430548 + 0.240109) or 0.842 in South Asia, etc.

Logged odds are weird; odds ratios are weird. Nobody thinks this way. Thinking about percentage-point-scale values is much easier. We can do this by calculating marginal effects instead and getting proportion-level changes in the outcome at specific values of GDP per capita or across the whole range of the fitted line.

Remember the fitted lines here—the effect or slope of GDP per capita changes depending on two things:

The region: the line is slightly higher and steeper in different regions (though not much here)
The level of GDP per capita: the line is shallower in richer countries; steeper in poorer countries

model_beta |> 
  plot_predictions(condition = c("gdp_per_cap", "region")) +
  geom_vline(xintercept = c(1000, 10000, 25000)) +
  scale_color_viridis_d(option = "plasma", end = 0.9) +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Predicted proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

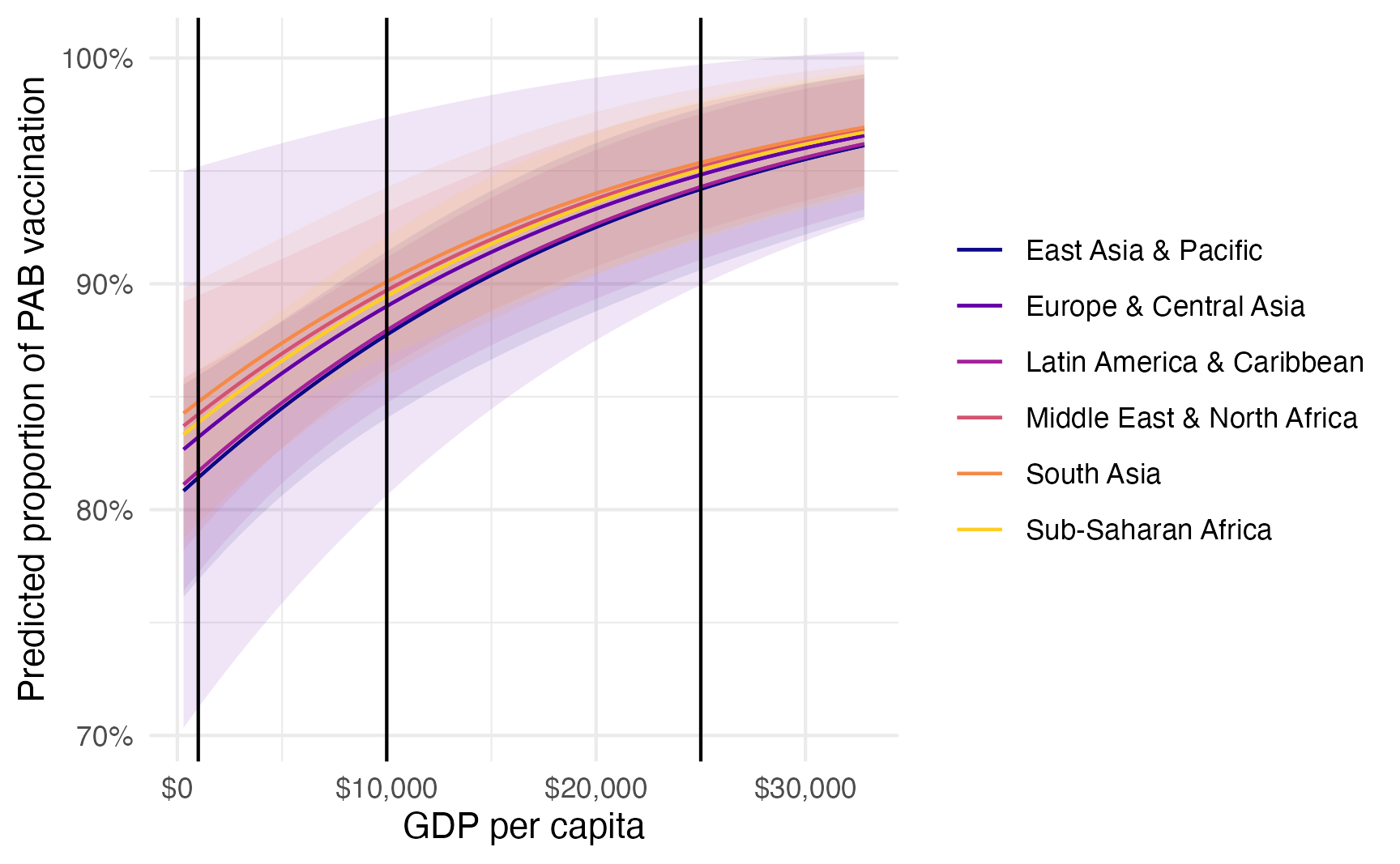
The effect of GDP per capita on the proportion of vaccinations is different when a country is poorer vs. richer. We can calculate proportion-level slopes at each of those points. These are going to look suuuuuper tiny because they’re based on \$1 changes in GDP per capita, so we’ll need to multiply them by 1000 to think of \$1,000 changes. We’ll also multiply them by 100 one more time since these are percentage point changes in the outcome:

model_beta |> 
  slopes(
    newdata = datagrid(gdp_per_cap = c(1000, 10000, 25000), region = unique),
    variables = "gdp_per_cap"
  ) |> 
  mutate(estimate = estimate * 1000 * 100) |> 
  as_tibble() |>  # The changed column disappears from the data.table printing :shrug:
  select(gdp_per_cap, region, estimate) |> 
  pivot_wider(names_from = region, values_from = estimate) |> 
  tt(caption = "Percentage point changes in the proportion of vaccinated children")

Percentage point changes in the proportion of vaccinated children
gdp_per_cap	South Asia	Europe & Central Asia	Middle East & North Africa	Sub-Saharan Africa	Latin America & Caribbean	East Asia & Pacific
1000	0.7	0.76	0.72	0.74	0.82	0.83
10000	0.49	0.53	0.5	0.51	0.58	0.59
25000	0.24	0.27	0.25	0.26	0.29	0.3

In South Asia, a \$1,000 increase in GDP per capita for super poor countries where GDP per capita is only \$1,000 (i.e. going from \$1,000 to \$2,000) is associated with a 0.69 percentage point increase in the vaccination rate, while in rich countries where GDP per capita is \$25,000, a \$1,000 increase (i.e. going from \$25,000 to \$26,000) is associated with only a 0.24 percentage point increase. The slope in richer countries is shallower.

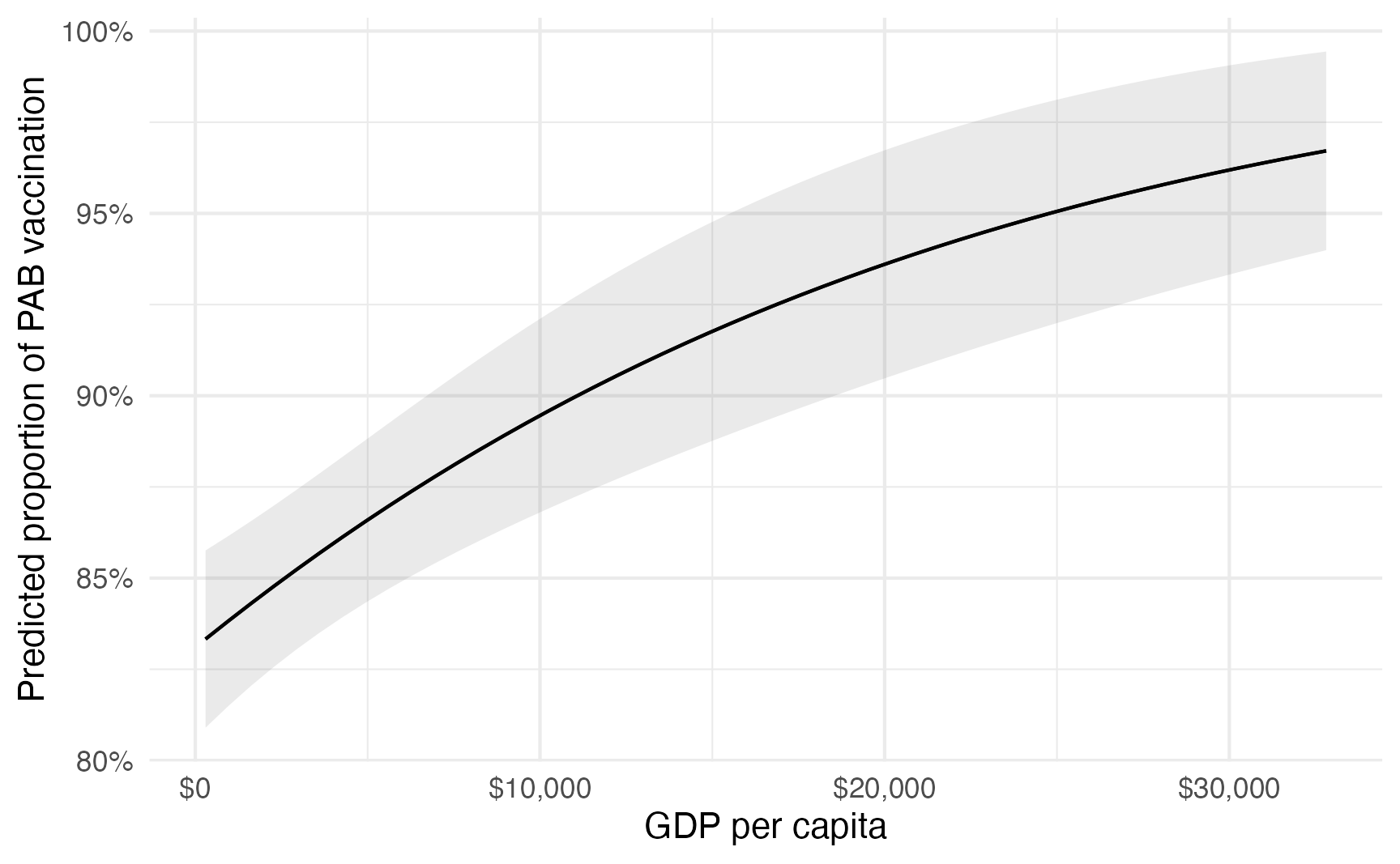
Instead of disaggregating everything by region and choosing arbitrary values of GDP per capita, we can also find the overall average slope of the line. Across all countries and regions different levels of GDP per capita, a $1,000 increase in GDP per capita is associated with a 0.665 percentage point increase in the proportion of vaccinated children, on average.

model_beta |> 
  avg_slopes(variables = "gdp_per_cap") |> 
  mutate(estimate = estimate * 1000 * 100) |> 
  as_tibble() |>
  select(estimate)
## # A tibble: 1 × 1
##   estimate
##      <dbl>
## 1    0.687

model_beta |> 
  plot_predictions(condition = "gdp_per_cap") +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Predicted proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

Bayesian Beta models

We can run this model with Bayesian regression too. We’ll set some weakly informative priors and define the model like this. If we had more data, we could also model the variance, or $\phi$, but we won’t here. (Here’s an example of modeling both the $\mu$ and the $\phi$)

\[ \begin{aligned} \text{PAB vaccination}_i &\sim \operatorname{Beta}(\mu_i, \phi_i) \\ \operatorname{logit}(\mu_i) &= \beta_0 + \beta_1\ \text{GDP per capita}_i + \beta_{2 \dots 6}\ \text{Region}_i \\ \\ \beta_0 &\sim \operatorname{Student t}(\nu = 3, \mu = 0, \sigma = 2.5) \\ \beta_{1 \dots 6} &\sim \mathcal{N}(0, 1) \end{aligned} \]

Here’s what those priors look like:

priors <- c(
  set_prior("student_t(3, 0, 2.5)", class = "Intercept"),
  set_prior("normal(0, 1)", class = "b")
)

priors |> 
  parse_dist() |> 
  ggplot(aes(y = 0, dist = .dist, args = .args, fill = prior)) +
  stat_slab(normalize = "panels") +
  scale_fill_viridis_d(option = "viridis", begin = 0.2, end = 0.8) +
  facet_wrap(vars(prior), scales = "free_x")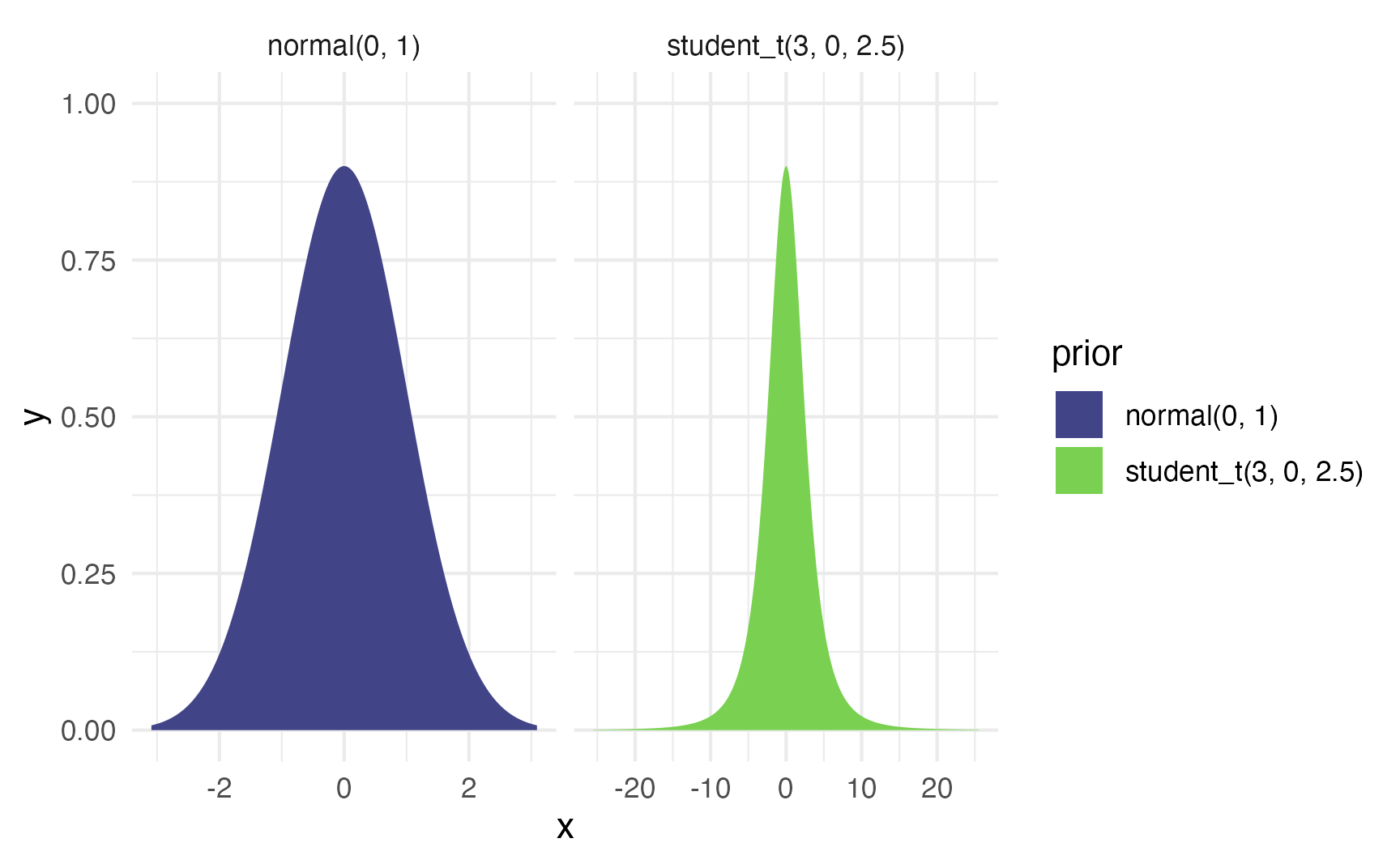

And here’s the model:

Code

model_beta_bayes <- brm(
  bf(
    prop_pab ~ log(gdp_per_cap) + region, 
    phi ~ 1
  ),
  data = tetanus_2010,
  family = Beta(),
  prior = priors,
  chains = 4, iter = 2000, seed = 1234,
  file = "models/model_beta_bayes"
)

Code

model_parameters(model_beta_bayes, verbose = FALSE) |> tt()

Parameter	Median	CI	CI_low	CI_high	pd	Rhat	ESS
b_Intercept	-0.303	0.95	-1.42	0.81	0.7	1	4339
b_phi_Intercept	2.838	0.95	2.55	3.1	1	1	5113
b_loggdp_per_cap	0.251	0.95	0.11	0.39	1	1	4085
b_regionEurope&CentralAsia	0.057	0.95	-0.74	1.06	0.55	1	4135
b_regionLatinAmerica&Caribbean	-0.033	0.95	-0.47	0.41	0.56	1	2963
b_regionMiddleEast&NorthAfrica	0.156	0.95	-0.32	0.62	0.73	1	3104
b_regionSouthAsia	0.234	0.95	-0.26	0.76	0.82	1	3530
b_regionSubMSaharanAfrica	0.232	0.95	-0.15	0.59	0.89	1	3001

We can visualize the posterior distribution for each coefficient:

model_beta_bayes |> 
  gather_draws(`^b_.*`, regex = TRUE) |>
  mutate(.value = exp(.value)) |>
  ggplot(aes(x = .value, fill = .variable)) +
  stat_halfeye(normalize = "xy") +
  scale_fill_viridis_d(option = "viridis", begin = 0.1, end = 0.9, guide = "none") +
  labs(x = "Coefficient value", y = NULL) +
  facet_wrap(vars(.variable), scales = "free_x") +
  theme(axis.text.y = element_blank())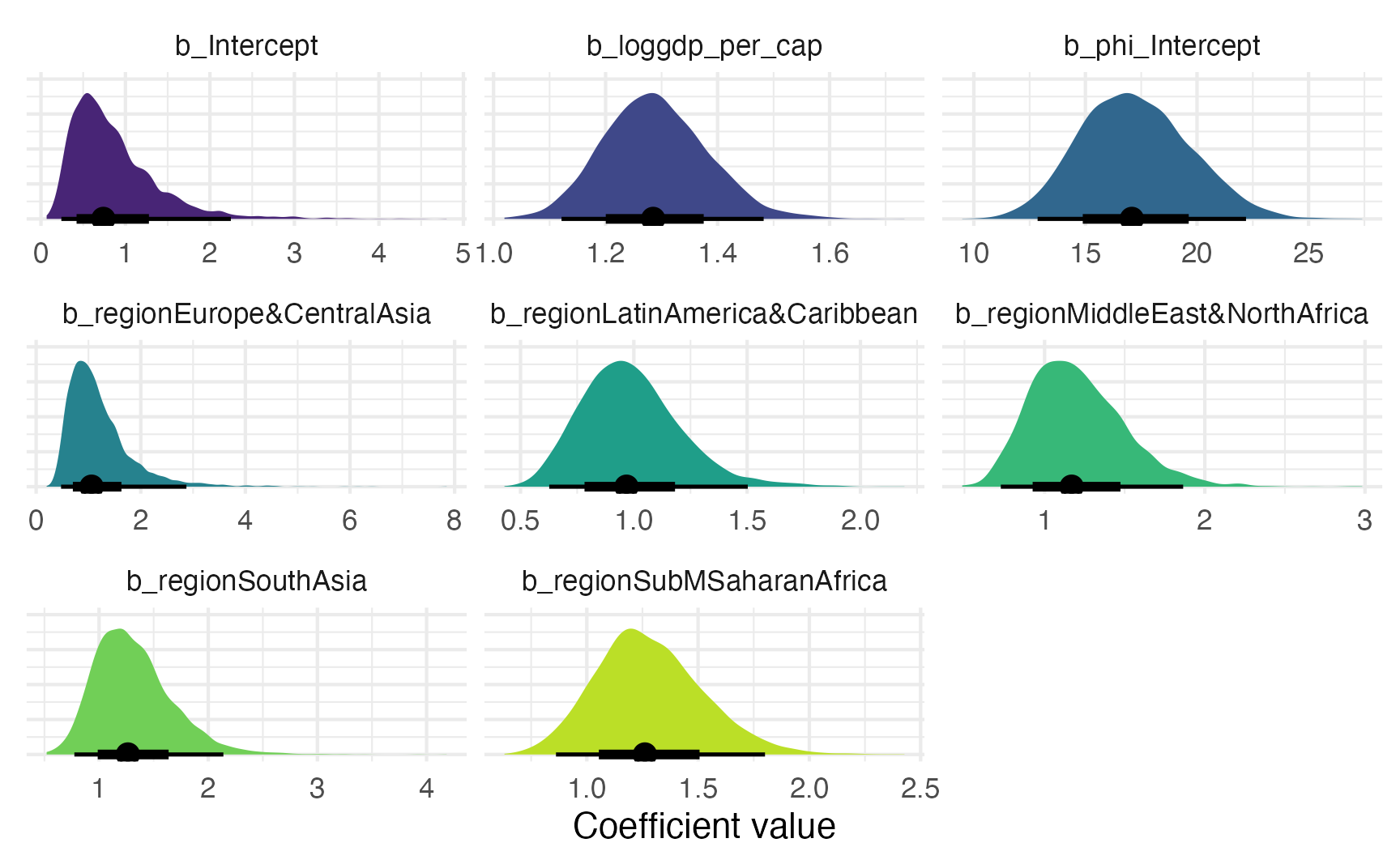

And we can see posterior predictions, either manually with {tidybayes}…

tetanus_2010 |>
  add_epred_draws(model_beta_bayes, ndraws = 50) |>
  ggplot(aes(x = gdp_per_cap, y = prop_pab, color = region)) +
  geom_point(data = tetanus_2010, size = 1) +
  geom_line(aes(y = .epred, group = paste(region, .draw)), 
    linewidth = 0.5, alpha = 0.3) +
  scale_color_viridis_d(option = "plasma", end = 0.9) +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Predicted proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

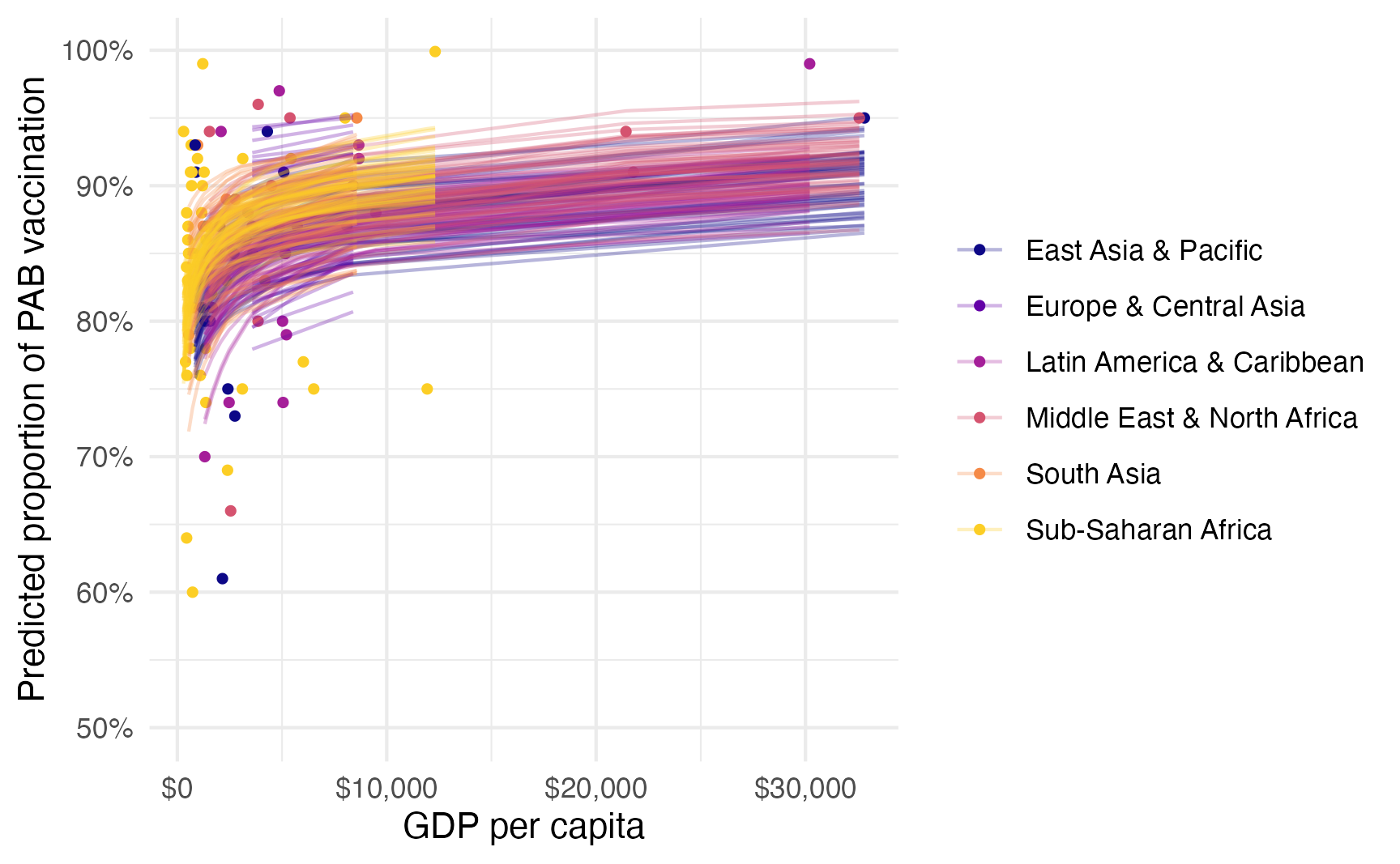
…or more automatically with {marignaleffects}:

model_beta_bayes |> 
  plot_predictions(condition = c("gdp_per_cap", "region")) +
  scale_color_viridis_d(option = "plasma", end = 0.9) +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Predicted proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

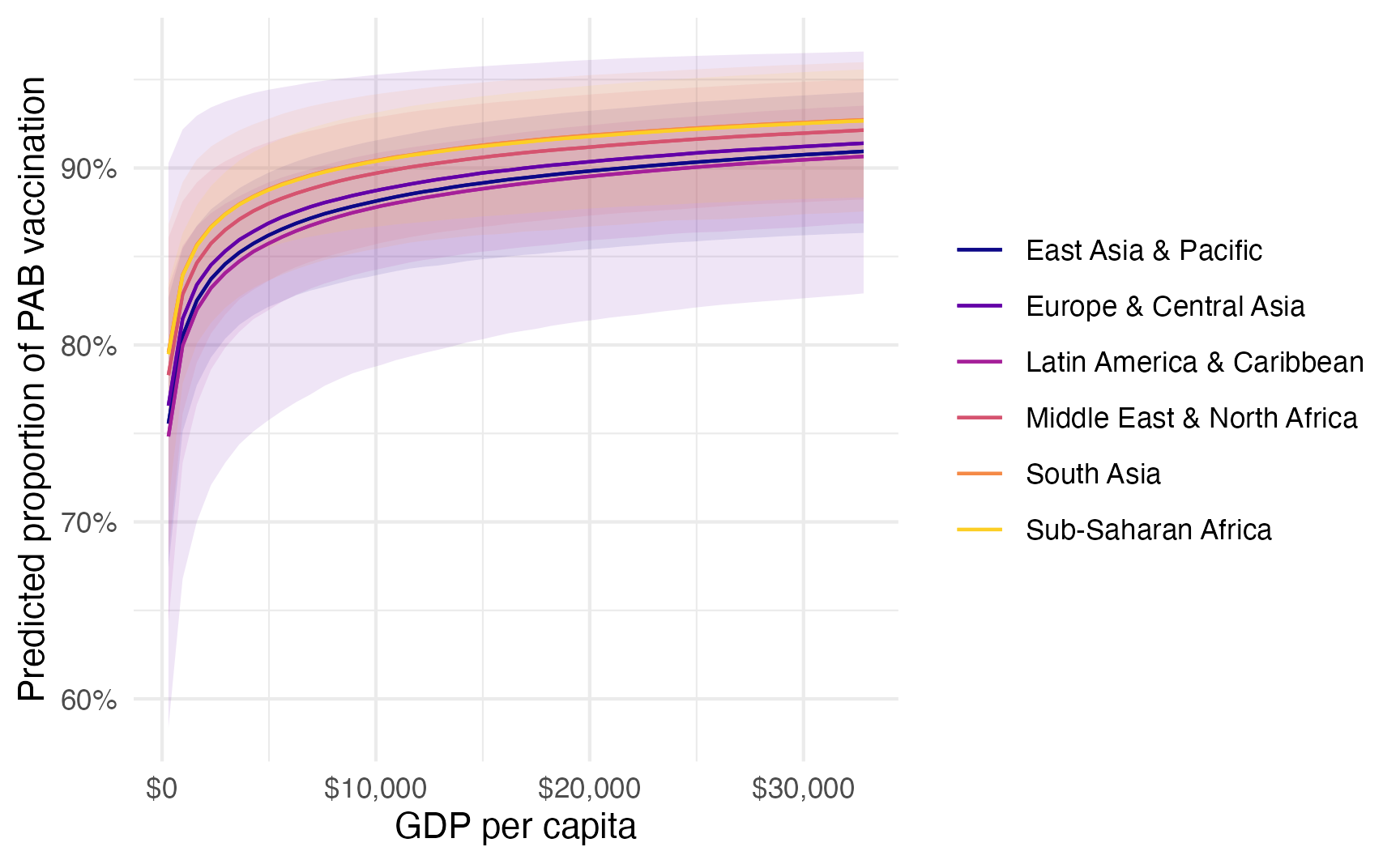
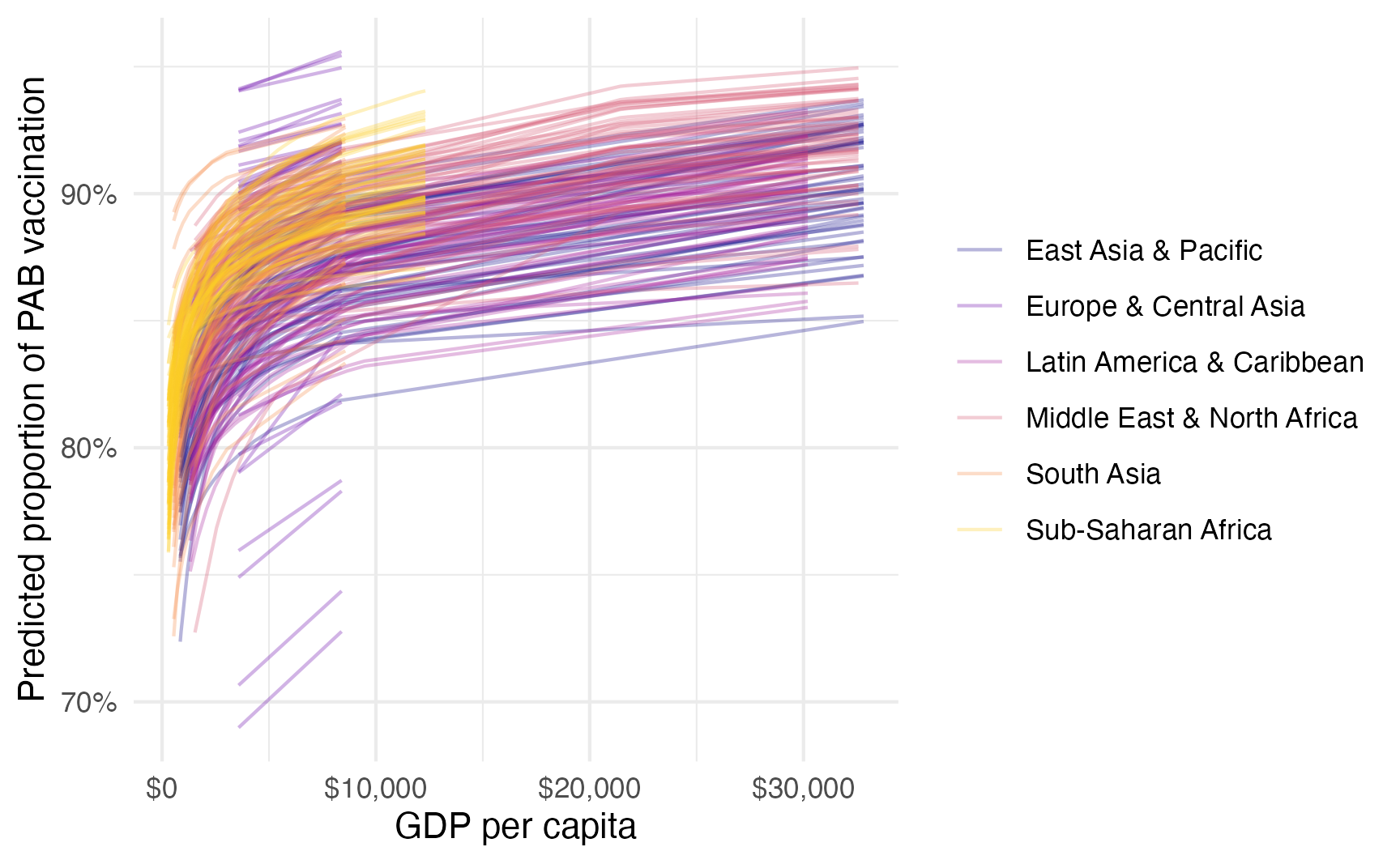
…or as a fancy spaghetti plot with {marginaleffects}:

model_beta_bayes |> 
  predictions(condition = c("gdp_per_cap", "region"), ndraws = 50) |>
  posterior_draws() |> 
  ggplot(aes(x = gdp_per_cap, y = draw, color = region)) +
  geom_line(aes(y = draw, group = paste(region, drawid)), 
    size = 0.5, alpha = 0.3) +
  scale_color_viridis_d(option = "plasma", end = 0.9) +
  scale_x_continuous(labels = label_dollar()) +
  scale_y_continuous(labels = label_percent()) +
  labs(
    x = "GDP per capita", 
    y = "Predicted proportion of PAB vaccination", 
    color = NULL, 
    fill = "Region"
  )

We can interpret the coefficients using marginal effects too. By themselves, we see posterior medians:

model_beta_bayes |> 
  slopes(
    newdata = datagrid(gdp_per_cap = c(1000, 10000, 25000), region = unique),
    variables = "gdp_per_cap"
  )
## 
##         Term gdp_per_cap                     region Estimate    2.5 %   97.5 %
##  gdp_per_cap        1000 South Asia                 3.31e-05 1.35e-05 5.85e-05
##  gdp_per_cap        1000 Europe & Central Asia      3.66e-05 1.13e-05 7.49e-05
##  gdp_per_cap        1000 Middle East & North Africa 3.52e-05 1.32e-05 6.62e-05
##  gdp_per_cap        1000 Sub-Saharan Africa         3.36e-05 1.50e-05 5.36e-05
##  gdp_per_cap        1000 Latin America & Caribbean  3.97e-05 1.54e-05 7.22e-05
##  gdp_per_cap        1000 East Asia & Pacific        3.89e-05 1.59e-05 6.66e-05
##  gdp_per_cap       10000 South Asia                 2.13e-06 1.07e-06 3.23e-06
##  gdp_per_cap       10000 Europe & Central Asia      2.40e-06 8.22e-07 4.83e-06
##  gdp_per_cap       10000 Middle East & North Africa 2.29e-06 1.07e-06 3.67e-06
##  gdp_per_cap       10000 Sub-Saharan Africa         2.16e-06 1.23e-06 2.78e-06
##  gdp_per_cap       10000 Latin America & Caribbean  2.66e-06 1.24e-06 4.18e-06
##  gdp_per_cap       10000 East Asia & Pacific        2.57e-06 1.32e-06 3.75e-06
##  gdp_per_cap       25000 South Asia                 6.96e-07 3.85e-07 1.03e-06
##  gdp_per_cap       25000 Europe & Central Asia      7.98e-07 2.90e-07 1.56e-06
##  gdp_per_cap       25000 Middle East & North Africa 7.53e-07 3.91e-07 1.14e-06
##  gdp_per_cap       25000 Sub-Saharan Africa         7.10e-07 4.54e-07 8.58e-07
##  gdp_per_cap       25000 Latin America & Caribbean  8.86e-07 4.61e-07 1.29e-06
##  gdp_per_cap       25000 East Asia & Pacific        8.55e-07 4.87e-07 1.18e-06
## 
## Type:  response 
## Columns: rowid, term, estimate, conf.low, conf.high, gdp_per_cap, region, predicted_lo, predicted_hi, predicted, tmp_idx, prop_pab

We can also visualize the posterior distributions of the specific marginal effects:

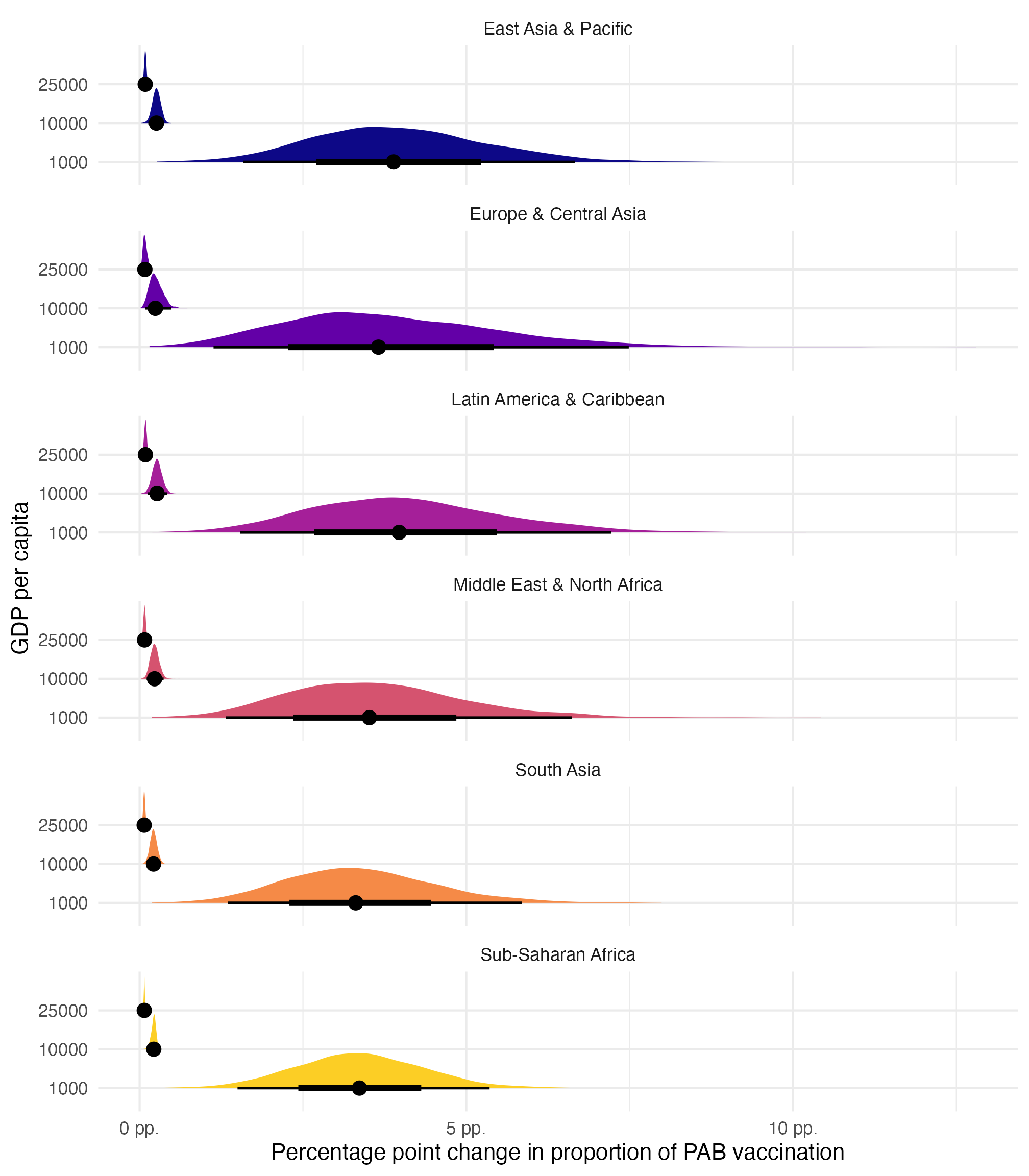
model_beta_bayes |> 
  slopes(
    newdata = datagrid(gdp_per_cap = c(1000, 10000, 25000), region = unique),
    variables = "gdp_per_cap"
  ) |> 
  posterior_draws() |> 
  mutate(draw = draw * 1000) |> 
  ggplot(aes(x = draw, y = factor(gdp_per_cap), fill = region)) +
  stat_halfeye(normalize = "xy") +
  scale_x_continuous(labels = label_number(scale = 100, suffix = " pp.")) +
  scale_fill_viridis_d(option = "plasma", end = 0.9, guide = "none") +
  facet_wrap(vars(region), ncol = 1) +
  labs(
    x = "Percentage point change in proportion of PAB vaccination", 
    y = "GDP per capita"
  )